Общие сведения об информации

1.1. Общие сведения об информации

Цифровые устройства являются составной частью всех ЭВМ, систем автоматического управления, автоматизированного управления и предназначены для обработки, хранения и передачи дискретной (цифровой) информации.

В узком смысле слова информация - отражение реального мира.

С точки зрения связистов и электронщиков – информация - это любые сведения, являющиеся объектом хранения, передачи и преобразования.

Информацию, воплощенную и зафиксированную в некоторой материальной форме, называют сообщением и передают с помощью сигналов.

Сигналом могут служить любые физические явления или объекты, изменение параметров которых во времени несет информацию в прямом или закодированном виде (свет, звук, напряжение, ток, давление, и т.д.).

В общем случае информационное сообщение может быть представлено в виде функции x(t). Причем эта функция может принимать любые вещественные значения в диапазоне изменения аргумента t. Например, изменение температуры во времени и т.д.

Информационное сообщение может иметь как непрерывный, так и дискретный характер (рис.1.1, а и 1.1, б соответственно). В автоматизированных системах управления и в технике связи для преобразования аналоговых сигналов в цифровую форму используются аналого-цифровые преобразователи (АЦП) различных типов, дельта-модуляторы.

Классы сигналов. Среди множества сигналов можно выделить два типа сигналов, используемых для передачи, обработки и хранения информации. Это аналоговый и дискретный сигналы.

Аналоговым называется сигнал, определенный для любого момента времени.

Дискретным называется сигнал, определенный только в дискретные моменты времени, например, через одну мсек. и т.д. Каждое значение дискретного сигнала может быть представлено числом любой приемлемой системы счисления. В цифровых системах представление дискретных значений сигнала числом, называется кодированием.

Кодирование чаще всего производится числами двоичной системы счисления.

Значение кодированного числа, представленное в привычной для нас десятичной системе счисления, определяет число уровней (Кn) квантования, т.е. дискретизации (рис. 1.2).

Шаг квантования (дискретизации) определяется как

.

Число разрядов двоичного числа m, соответствующего Кn, определяется как

,

т.е. как целая часть логарифма максимального значения числа Кnmax, дополненного единицей.

Основы алгебры логики

1.4. Основы алгебры логики

Алгебра логики (АЛ) является основным инструментом синтеза и анализа дискретных автоматов всех уровней. АЛ называют также Булевой алгеброй. АЛ базируется на трёх функциях, определяющих три основные логические операции.

1. Функция отрицания (НЕ). f1 =`X читается, как f1 есть (эквивалентна) НЕ Х. Элемент, реализующий функцию НЕ, называется элементом НЕ (инвертором).

Элемент НЕ имеет два состояния.

2. Функция логического умножения (конъюнкции). Функция логического умножения записывается в виде f2=X1·X2. Символы логического умножения &, L, <×>, ´. Функция конъюнкции читается так: f2 есть (эквивалентна) Х1 и Х2, поскольку функция истинна тогда, когда истинны 1-й и 2-й аргументы (переменные). Конъюнкцию называют функцией И, элемент, реализующий эту функцию, элементом И.

В общем случае функцию логического умножения от n переменных записывают так:

Количество переменных (аргументов), участвующих в одной конъюнкции, соответствует количеству входов элемента И.

3. Логическое сложение (дизъюнкция). Функция логического сложения записывается в виде f3=X1 + X2, и читается так: f3 есть Х1 или Х2, поскольку функция истинна, когда истинна одна или другая переменная (хотя бы одна). Поэтому функцию дизъюнкции часто называют функцией ИЛИ. Символы логического сложения +,V.

В общем случае функция ИЛИ записывается:

Используя операции (функции) И, ИЛИ, НЕ можно описать поведение любого комбинационного устройства, задав сколь угодно сложное булево выражение. Любое булево выражение состоит из булевых констант и переменных, связанных операциями И, ИЛИ, НЕ.

Пример булева выражения:

Основные законы алгебры логики. Основные законы АЛ позволяют проводить эквивалентные преобразования функций, записанных с помощью операций И, ИЛИ, НЕ, приводить их к удобному для дальнейшего использования виду и упрощать запись.

ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ Таблица 1.1

N	а	б	Примечание
1 2 3 4 5	=1 X+0=X X+1=1 X+X=X X+ =1	=0 X1=X X0=0 XX=X X =0	Аксиомы (тождества)
6	=X		Закон двойного отрицания
7	X+Y=Y+X	XY=YX	Закон коммутативности
8	X+X*Y=X	X =X	Закон поглощения
9	= *		Правило де-Моргана (закон дуальности)
10	+Z=X+Y+Z		Закон ассоциативности
11	X+Y*Z=		Закон дистрибутивности

Булевой алгебре свойственен принцип двойственности, что наглядно иллюстрирован в табл. 1.1. Как следует из табл. 1.1, только закон двойного отрицания не подчиняется этому принципу.

Используя законы алгебры логики, можно упростить булевы выражения, в частности, правило склеивания позволяет упростить выражение типа

.

         Действительно, используя законы 2, 5 и 11 можно записать исходное выражение в виде Х2(Х1 +`Х1 ) =Х2. Так как логическая операция Х1 +`Х1 = 1 (см. з-н 5), а Х2×1 = Х2 (см. з-н 2б), полученное выражение истинно.

         Способы задания функций алгебры логики. При сопоставлении функций АЛ с дискретными автоматами аргументы функций, сопоставляются с входами, а сами функции с выходами дискретного автомата.

         Поскольку дискретный автомат имеет конечное число входов, то мы будем иметь дело с функцией конечного числа аргументов. Если автомат имеет m входов, то количество входных переменных тоже m и число возможных комбинаций наборов значений этих входных аргументов (переменных) К=2m.

         Поскольку автомат имеет конечное число входов, его состояние описывается конечным числом значений функций выходов. Существует несколько способов задания функций АЛ и дискретного автомата.

         1. Табличный способ. При этом способе функция задается в виде таблицы истинности, представляющей собой совокупность всех наборов переменных и соответствующих им значений функции.

Таблица истинности содержит 2m строк, m столбцов (по количеству входов) и один столбец для записи значения функции.

Например: пусть требуется задать функцию трех переменных F1(Х1,Х2,Х3) (рис. 1.4), т.е. автомат на три входа и на один выход, следовательно, M=3, К=8.

Следующий способ задания дискретного автомата – числовой. В Этом случае функция задается в виде десятичных эквивалентов номеров наборов аргументов, при которых функция принимает единичное значение. Например, для рассмотренного выше примера функция F1 принимает единичные значения на наборах переменных со следующими номерами: 1, 2, 5, тогда числовой способ задания будет иметь вид

.

Координатный способ. При этом способе дискретный автомат задается с помощью карты его состояния, которая известна как карта Карно.

Карта Карно содержит 2m клеток по числу наборов значений переменных. Каждая клетка определяется координатами строк и столбцов, соответствующими определенному набору переменных. Все входные переменные разбиваются на 2 группы так, что одна группа определяет координаты строк, а другая - координаты столбцов. В каждой клетке карты Карно проставляется соответствующее значение функции на заданном наборе. Пример задания функции трех переменных приведен на рис. 1.5. Числовое выражение этой функции выглядит так:

Пример построения карты Карно для функции 4-х переменных.

Пусть функция задана в числовой форме и имеет вид:

,

следовательно, К=16, m=4.

Сначала проводим разметку координат карты Карно без указания значений функции. Для удобства воспользуемся указанием "шапки" в виде прямых линий, “под” которыми переменные входят в значение координат без отрицания (рис.1.6). Таким образом, по столбцам и по строкам переменные входят без отрицания в пределах линии-шапки.

Для наглядности координаты клеток карты Карно указаны в трех формах: в виде наборов переменных; в виде двоичного числа, соответствующего порядковому номеру набора переменных; в десятичном эквиваленте номеров наборов переменных. На практике координаты внутри клеток не записывают (рис. 1.7), в клетках указываются единичные значения функции, соответствующие “координатным” наборам переменных. Нулевые значения функции в клетки можно не записывать, т.е. клетки, координаты которых определяются наборами переменных с нулевыми значениями функции, можно оставить пустыми.

Следует отметить, что перестановка местами переменных Х1 и Х2, а так же переменных Х3 и Х4 допускается, допускается также перестановка местами переменных Х1Х2 и Х4Х3. При построении карты Карно, т.е. при задании логической функции, указывают лишь внешние элементы разметки координат (рис. 1.7).

Аналитический способ задания функции алгебры логики. При этом способе функция задается в виде аналитического выражения, полученного путем применения каких-либо логических операций.

Например:

.

Совершенная нормальная дизъюнктивная форма (СНДФ). По таблице истинности можно составить логическое выражение, содержащее наборы переменных, в которые входят все переменные с отрицанием или без. Одна из его форм называется СНДФ.

В качестве примера получения СНДФ рассмотрим случай задания логической функции в виде таблицы истинности.

Пусть задана функция трех переменных. Таблица истинности этой функции показана на рис. 1.8. (очевидно, что значения функции взяты произвольно и могут быть любыми).

Из таблицы истинности видно, что функция принимает значение логической единицы только на трех наборах переменных, т.е. на 2, 4 и 5-м наборах. Для второй строки (второго набора переменных) можно записать: Х1=0, Х2=1, Х3=0, следовательно, функция f(0,1,0)=1. Принято (по умолчанию) считать, что если переменная в "нормальном" состоянии имеет значение логической единицы, а в инверсном - логического нуля, тогда функцию для второй строки можно представить в виде `X1Х2X3 = 1. Для четвертой строки - `X1X2Х3 = 1 и для пятой строки - Х1X2Х3 = 1. Аналитическое выражение функции выглядит как

.

Каждое произведение содержит все три переменные с отрицанием или без отрицания и соответствует только одной строке набора переменных, на котором функция принимает значение логической единицы. Произведения, в которых содержатся все переменные с отрицанием или без, называются конституентами единицы или минтермами. Функция будет представлять логическую сумму всех произведений, равных логической единице. В нашем примере вся сумма (дизъюнкция) соответствует совокупности произведений переменных для трех строк.

СНДФ любой функции записывается по таблице истинности согласно следующему правилу.

Для каждого набора переменных, на которых функция принимает значение логической 1, записываются конституенты, и все эти конституенты объединяются дизъюнктивно.

Переменные каждой строки, имеющие значение логического 0, в конституенты входят с отрицанием (записываются в произведение в инвертированном виде), а переменные, имеющие значения логической 1 - без отрицания.

Любую логическую (булеву) функцию можно представить дизъюнкцией конституент.

Если одно из произведений не содержит хотя бы одной переменной, то такая форма называется нормальной дизъюнктивной формой (НДФ).

Например:

.

Совершенная нормальная конъюнктивная форма (СНКФ). СНКФ можно построить по таблице истинности также как СНДФ. Для чего все значения функции представляют в инверсном виде и записывают СНДФ для инверсной функции. Далее, используя закон де Моргана, получают конъюнкцию всех дизъюнкций. В каждую дизъюнкцию входят все переменные строки таблицы, для которой функция до инвертирования принимала значение логической 1.

Если (хотя бы одна) дизъюнкции, которые называются также макстермами (конституентами нуля), не содержат отдельные переменные, то такая форма записи функции называется нормальной конъюнктивной формой (НКФ).

Пример записи СНКФ. Пусть функция представлена в виде таблицы истинности (рис. 1.9).

Элементарные функции алгебры-логики. Среди всех функций алгебры логики особое место занимают функции одной и двух переменных, называемые элементарными. В качестве логических операций над переменными, эти функции позволяют реализовать различные функции от любого числа переменных.

Общее количество функций АЛ от m переменных R=2k, где k=2m. Рассмотрим элементарные функции от двух переменных

Переменные и их состояния	Обозначение функции	Назначение Функции
X1 X2	0 0	0 1	1 0	1 1
f0	0	0	0	0	f0=0	Генератор 0
f1	0	0	0	1	f1=X1·X2	«И»
f2	0	0	1	0	f2=X1·
f3	0	0	1	1	f3=X1
f4	0	1	0	0	f4= ·X2
f5	0	1	0	1	f5=X2
f6	0	1	1	0	f6=X1 X2	Сумматор по модулю два
f7	0	1	1	1	f7=X1+X2	«ИЛИ»
f8	1	0	0	0	f8=	«ИЛИ-НЕ»
f9	1	0	0	1	f9=X1~X2	Функция равнозначности
f10	1	0	1	0	f10=	«НЕ» Х2
f11	1	0	1	1	f11=X1+
f12	1	1	0	0	f12=	«НЕ» Х1
f13	1	1	0	1	f13= +X2
f14	1	1	1	0	f14=	«И-НЕ»
f15	1	1	1	1	f15=1	Генератор 1

Полная система логических функций

1.5. Полная система логических функций. Понятие о базисе

Функционально полная система логических функций представляет собой набор логических функций, с помощью которых можно записать любую, сколь угодно сложную функцию. В этом случае говорят, что этот набор образует базис. Функционально полными являются 3 базиса:

1) "И-ИЛИ-НЕ" (базис конъюнкции, дизъюнкции, инверсии)

2) "И-НЕ" (базис Шеффера)

3) "ИЛИ-НЕ" (базис Пирса или функция Вебба).

Элементы, реализующие операцию "И-НЕ", “ИЛИ-НЕ” и “Исключающее ИЛИ” на принципиальных и структурных схемах изображаются так:

Примеры реализации логических операций в базисах “И-НЕ” и “ИЛИ-НЕ”.

Реализация операции “НЕ”:

Реализация операции “И”:

Реализация операции “ИЛИ”:

Пример реализации комбинационного устройства в базисе "И-НЕ". Пусть задана функция, реализуемая комбинационным устройством, в аналитической форме

Используя закон де Моргана и с учетом закона двойного инвертирования, запишем эту функцию в виде

Как следует из полученного аналитического выражения, логическое устройство должно содержать три двухвходовых и один трехвходовой элемент И-НЕ. Функциональная схема комбинационного устройства, построенная в базисе И-НЕ, показана на рис. 1.10.

Представление чисел в современных цифровых устройствах

имеют значения 1, 16, 256, 4096, и т.д.

         Двоичная система счисления. Понятие весовых коэффициентов сохраняется и для чисел двоичной системы счисления (основание Р = 2). Рассмотрим пример, где число представлено в двоичной системе счисления и имеет вид 11011012 (индекс "2" в конце числа показывает, что число представлено в двоичной системе счисления). Десятичный эквивалент этого числа, т.е. значение числа в привычной для нас системе счисления, определим, используя весовые коэффициенты разрядов символов

11011012 =1·26 + 1·25 + 0·24 + 1·23 + 1·22 + 0·21 + 1·20 =

= 1·64 + 1·32 + 0·16 + 1·8 + 1·4 + 0·2 + 1·1 = 10910.

Таким образом, десятичный эквивалент двоичного числа определяется как сумма весовых коэффициентов разрядов, имеющих единичный сомножитель.

В цифровой технике часто используется и двоично-десятичная система счисления. При этом каждый разряд десятичного числа представляется четырьмя разрядами двоичного числа. Очевидно, что при этом используются не все значения четырехразрядного двоичного числа, т.к. оно может реализовать числа от 0 до 15, а в двоично-десятичной системе используется лишь значения от 0 до 9.

         Арифметические основы цифровых устройств. При выполнении различных операций в современных цифровых устройствах и системах числа обычно представляются в двоичной системе счисления. Это связано с тем, что для представления смысла символов цифр двоичной системы счисления можно использовать простые электронные схемы с двумя электрическими состояниями. Принято, что символ “1” представляется некоторым стандартным уровнем напряжения или тока, а “0” - нулевым или близким к нулю уровнем напряжения или тока.

         Арифметические операции над двоичными числами могут производиться по тем же правилам, что и над десятичными, однако, с целью упрощения цифровых систем для выполнения арифметических операций применяют алгоритмы, отличные от алгоритмов действий десятичной арифметики.

         В двоичной системе счисления для представления знака числа используется дополнительный знаковый разряд (один или несколько разрядов), который располагается перед старшим числовым разрядом. Для положительных чисел значение знакового разряда Зн.р.=0, для отрицательного числа Зн.р.=1.

         Операция вычитания в цифровых системах реализуется с помощью операции сложения. Вычитаемое при этом представляется в дополнительном коде (если расчет не требует высокой точности - в обратном коде).

         Двоичный код со знаком называют также прямым кодом. В качестве примера рассмотрим положительное и отрицательное числа, десятичный эквивалент которых равен 4610.

Обратный код получается путем замены всех “0” на “1” и всех “1” на “0” прямого кода (двоичного числа со знаком). Причем, знаковый разряд при этом остается неизменным.

Замена “0” на единицу (“1”) называется инвертированием (также и замена “1” на “0”).

Обратный код, дополненный единицей в младшем разряде, называется дополнительным кодом. Последовательность действий при получении дополнительного кода:

Сложение и вычитание двоичных чисел. Правила сложения двух двоичных чисел можно показать на следующем примере:

Пример сложения многоразрядных чисел. Требуется сложить два числа 1810 и 2310

Вычитание в цифровых устройствах производится также как и сложение, только вычитающее представляется в дополнительном коде. Рассмотрим два примера, в первом требуется из числа 23 отнять число 18, а во втором из 18 отнять 23. С начала вычитающие представим в дополнительном коде

Перевод отрицательного дополнительного кода в отрицательный прямой код осуществляется также, как и перевод в дополнительный код прямого кода. Тогда

В результате полученное число соответствует числу минус пять (-5).

Принято считать, что дополнительный код положительного числа совпадает с его прямым кодом.

Операция вычитания с использованием только обратного кода (без дополнительных операций по переводу его в дополнительный код) приводит к ошибке, определяемой единицей в младшем разряде, и поэтому при точных расчетах не применяется.

1.2. Представление чисел в современных цифровых устройствах

         Системы счисления. Система счисления - это код, в котором использованы специальные символы для обозначения количества каких либо объектов. Количество символов в системе счисления носит название его основания. Например, система счисления с основанием 10 имеет десять символов от 0 до 9. Система счисления с основанием два содержит всего два символа, эта система называется двоичной системой счисления. В шестнадцатеричной системе используется 16 символов и т.д.

         Чем меньше основание системы счисления, тем больше разрядов требуется для представления одного и того же количества объектов. Количественное значение символа определяется его номером разряда, т.е. местом расположения этого символа в числовом ряду.

         Десятичная система счисления. Основание этой системы счисления Р=10, так как для записи цифр разрядов используется десять символов. В качестве примера возьмем десятичное число 523.0. Здесь цифра 5 обозначает число 500, так как оно занимает по порядку 3-й разряд слева от десятичной точки.

            523 = 5•102 + 2•101 + 3•100   - отсюда следует, что каждый разряд имеет свой “вес”. В зависимости от номера разряда (т.е. от номера позиции символов) разряды имеют следующие весовые коэффициенты

Таким образом, весовой коэффициент разряда в общем случае определяется как Рn-1, где n-порядковый номер разряда после точки (для целых чисел обычно точка не указывается, но подразумевается). Разряды справа после точки имеют следующие веса: Р-1, Р-2, и т.д.

Шестнадцатеричная система счисления. Основание этой системы Р = 16 и для записи цифр разрядов используются 16 символов 0, 1, 2, . . . 9, А, В, С, D, Е, F. Весовые коэффициенты определяются как Рn-1, т.е.

Вопросы и задания

1.1. Какие виды сигналов используются в информационных системах?

1.2. Числа какой системы счисления используются в вычислительной технике?

1.3. Как связаны законы алгебры логики и работа элементов цифровой логики?

1.4. Как понять смысл “задания” функций АЛ?

1.5. Какие законы АЛ отражают суть понятий о базисе?

1.6. Нарисуйте схему цифрового логического замка в базисе И-НЕ, в которой сигнал на выходе замка принимает значение лог. “1” (Z= 1) при выполнении условия Х1=0; Х2=1; Х3=1; X4=1; X5=0 X6=1.

Анализ комбинационных устройств

2.10. Анализ комбинационных устройств

Анализ - это процесс получения логического выражения для существующего комбинационного устройства, т.е. при анализе необходимо получить оптимальное логическое выражение (если требуется и СНДФ) имеющейся логической схемы.

Необходимость в анализе КУ возникает при модернизации логических устройств, обновлении элементной базы, а также при оптимизации схемы цифрового автомата.

Рассмотрим пример анализа простейшего логического устройства. Пусть дан фрагмент схемы комбинационного устройства, приведенный на рис. 2.31. Требуется минимизировать логическое выражение, реализуемое этой схемой и синтезировать новую схему в базисе “И-НЕ”.

В начале анализа присваиваем имена промежуточным функциям на выходе каждого элемента и запишем логические выражения для этих функций

Z1 =

1; Z2 =

; Z3 = Z1 + Z2 =

1 +

;

Z4 = Z3 X1 = (

)X1 + X1

1 = X1

Выходная функция КУ представляет дизъюнкцию трех переменных (функций Z2, Z4 и Х4) с последующей инверсией

Y =

Для удобства в преобразовании функцию Y представим в инверсном виде (а в конце процесса анализа снова вернём в исходный вид), тогда

= X4 +

+ X1

Используя закон де Моргана, преобразуем инверсию конъюнкции

в дизъюнкцию инверсий т.е.

2 +

С учетом правил преобразования функцию Y приведем к виду

= X4 +

2 +

3 + X1 (

2 +

3) = X4 +

2 +

3 +X1

2 + X1

= Х4 +

2(1 + X1) +

3(1 + X1) = X4 +

2 +

Вернём функцию в исходную форму, т. е. снова проинвертируем

Y =

Полученная функция соответствует минимальной форме и содержит всего одну конъюнкцию. Очевидно, в общем случае может получиться сложное логическое выражение, требующее минимизации с использованием известных методов, в частности карт Карно.

Рис. 2.31 Фрагмент схемы комбинационного устройства с указанием промежуточных функций

Схема вновь построенного комбинационного устройства в базисе “И-НЕ” приведена на рис. 2.32.

Из рис. 2.32 следует, что для реализации операции отрицания переменных Х3 и Х4 использованы элементы “И - НЕ” с объединенными входами. Такой же элемент использован для отрицания промежуточного результата функции после элемента “3И-НЕ”.

Рис. 2.32. Фрагмент схемы КУ, приведенный в базис И-НЕ

Схема КУ, приведенная в единый элементный базис обладает большей устойчивостью, так как количество переменных сократилось (в результате упрощения “выпала” переменная Х1).

Дешифраторы

2.4. Дешифраторы

Линейный или одноступенчатый дешифратор. Дешифратор - это комбинационное устройство, предназначенное для преобразования параллельного двоичного кода в унитарный, т.е. позиционный код. Обычно, указанный в схеме номер вывода дешифратора соответствует десятичному эквиваленту двоичного кода, подаваемого на вход дешифратора в качестве входных переменных, вернее сказать, что при подаче на вход устройства параллельного двоичного кода на выходе дешифратора появится сигнал на том выходе, номер которого соответствует десятичному эквиваленту двоичного кода. Отсюда следует то, что в любой момент времени выходной сигнал будет иметь место только на одном выходе дешифратора. В зависимости от типа дешифратора, этот сигнал может иметь как уровень логической единицы (при этом на всех остальных выходах уровень логического 0), так и уровень логического 0 (при этом на всех остальных выходах уровень логической 1). В дешифраторах каждой выходной функции соответствует только один минтерм, а количество функций определяется количеством разрядов двоичного числа. Если дешифратор реализует все минтермы входных переменных, то он называется полным дешифратором (в качестве примера неполного дешифратора можно привести дешифратор двоично-десятичных чисел).

Рассмотрим пример синтеза дешифратора (полного) 3 ® 8, следовательно, количество разрядов двоичного числа - 3, количество выходов - 8.

Таблица состояний дешифратора

Х3 Х2 Х1

Z0 Z1 Z2 Z3 Z4 Z5 Z6 Z7

0 0 0

0 0 1

0 1 0

0 1 1

1 0 0

1 0 1

1 1 0

1 1 1

1 0 0 0 0 0 0 0

0 1 0 0 0 0 0 0

0 0 1 0 0 0 0 0

0 0 0 1 0 0 0 0

0 0 0 0 1 0 0 0

0 0 0 0 0 1 0 0

0 0 0 0 0 0 1 0

0 0 0 0 0 0 0 1

7Как следует из таблицы состояния, каждой функции соответствует только один минтерм, следовательно, не требуется минимизировать эти функции (рис. 2.9).

Из полученных уравнений и схемы дешифратора следует, что для реализации полного дешифратора на m входов (переменных) потребуются n = 2m элементов конъюнкции (количество входов каждого элемента “И” равно m)и m элементов отрицания.

Пирамидальные дешифраторы. Пирамидальные дешифраторы позволяют реализовать схему на базе только двухвходовых элементов логического умножения (конъюнкции). Рассмотрим пример реализации дешифратора 3®8

Для построения такого дешифратора потребуется 12 двухвходовых элементов 2И и три инвертора. Пирамидальные дешифраторы при больших количествах входных переменных позволяют несколько упростить конструкцию устройства, т.е. уменьшить количество интегральных микросхем.

Промышленностью стран СНГ, в том числе и России, выпускаются различные модификации дешифраторов в интегральном исполнении. Обозначение дешифраторов на принципиальных схемах показано на рис. 2.10.

Двухступенчатые дешифраторы на интегральных микросхемах. Пример дешифратора для пятиразрядного двоичного кода. Каждый дешифратор выполнен с управляющими входами, объединенными конъюнктивно. При выполнении условия конъюнкции на выходе, номер которого соответствует десятичному эквиваленту двоичного кода, появится уровень логического “0”. В противном случае все выходы находятся в состоянии логической единицы (рис.2.11). Как следует из рис. 2.11, пятиразрядный дешифратор, имеющий 32 выхода, выполнен на базе четырех дешифраторов с использованием лишь одного дополнительного инвертора, что достигнуто благодаря наличию входной управляющей логики каждой интегральной микросхемы.

Нетрудно заметить, что входная логика дешифраторов КР1533ИД7 позволяет реализовать функцию дешифратора 2®3 без дополнительных элементов, а полного дешифратора 2®4 с использованием одного инвертора.

Гонки в комбинационных устройствах

е. безынерционные, ( что на практике достичь не удается), на выходе схемы КУ импульс помехи отсутствует. Однако в реальных схемах всегда имеет место явление гонок и требуется создать такие схемы, в которых влияние этого явления устраняется.

         Борьба с гонками. Существует три наиболее часто встречающихся способа борьбы с гонками:

         - тактирование;

         - построение противогоночных схем;

- учет минимального времени задержки распространения сигнала. Пример реализации тактирования цикла работы комбинационного устройства (рис.2.4).

2.2. Гонки в комбинационных устройствах

Комбинационное устройство (КУ) - это устройство с m входами и n выходами. Если КУ выполнено на базе идеальных, т.е. безинерционных элементов, состояние выходов однозначно определяется состоянием входов в тот же момент времени. Однако, инерционность элементов и наличие различных факторов, приводящих к задержке распространения сигнала, приводят к задержке появления выходных сигналов КУ, т.е. сигналы на выходе КУ, соответствующие новому состоянию входных сигналов, появляются не сразу, а с некоторой задержкой. При этом в переходный период возможно появление на выходах устройства некоторых промежуточных значений сигналов, не соответствующих заданному состоянию устройства. Такое явление получило название состязаний или гонок. Обычно, вырабатываемые узлами КУ промежуточные значения сигналов, представляют собой импульсы очень малой длительности, являющиеся помехой для всей цифровой системы. Они могут запускать непредусмотренное срабатывание триггеров, счетчиков и осуществлять нежелательные записи в регистры.

Рассмотрим в качестве примера фрагмент схемы комбинационного устройства (рис. 2.1), где может наблюдаться явление гонок. Для наглядности процесса формирования промежуточного значения выходного сигнала приведены временные диаграммы состояний различных цепей распространения в идеальном и реальном случаях (рис.2.2, рис. 2.3).

Время задержки импульсов в цепях определяется средним временем задержки распространения сигнала всеми элементами этой цепи. Момент времени появления импульса помехи определяется соотношением числа инвертирующих элементов в конкурирующих цепях фрагмента схемы КУ (см. рис.2.2, а и рис.2.3). Как следует из рис.2.2, а, если элементы схемы идеальные, т.

Многоразрядный сумматор с последовательным

Входы	Промежуточные величины	Выходы
ai	bi	сi	Pi	gi	ri	Si	Ci+1
0	0	0	0	0	0	0	0
0	1	0	1	0	0	1	0
1	0	0	1	0	0	1	0
1	1	0	0	1	0	0	1
0	0	1	0	0	0	1	0
0	1	1	1	0	1	0	1
1	0	1	1	0	1	0	1
1	1	1	0	1	0	1	1

Для сложения двух многоразрядных двоичных чисел на каждый разряд необходим один полный сумматор. Только в младшем разряде можно обойтись полусумматором. На рис. 2.23 приведена схема, предназначенная для сложения двух четырехразрядных чисел А и В. Эта схема выпускается в интегральном исполнении. В ее младшем разряде также используется полный сумматор, чтобы иметь возможность наращивания разрядности схемы.

Рис. 2.23. Сумматор с последовательным переносом

Мультиплексоры

Если Х1=Х2=0, на выход мультиплексора будет передаваться сигнал с входа D0. Когда на адресных (управляющих) входах Х1=1 и Х2=0, то на выход будет передаваться сигнал с входа D1 и т.д.

         Мультиплексоры нашли широкое применение в вычислительной технике в качестве коммутаторов цифровых сигналов. Они используются в компьютерах и микропроцессорных контроллерах для коммутации адресных входов динамических оперативных запоминающих устройств, в узлах объединения или разветвления шин и т.д. На базе мультиплексоров можно построить различные комбинационные устройства с минимальным числом дополнительных элементов логики. Следует отметить, что мультиплексоры хотя, и предназначены для коммутации цифровых сигналов, но с помощью мультиплексоров, изготовленных по КМОП технологии, можно коммутировать и аналоговые сигналы.

         Универсальные логические модули (УЛМ) на МS. Кроме ком-мутационных функций, мультиплексоры позволяют реализовать комбинационные устройства на m (m-количество управляющих входов) входов и на один выход. Если комбинационное устройство, построенное на базе мультиплексора, не требует подключения дополнительных элементов логики, оно называется универсальным логическим модулем. Отметим, что мультиплексор 8 ®1 (3 управляющих и 8 информационных входов) позволяет реализовать любую функцию трёх переменных.

         Для получения УЛМ управляющие входы мультиплексора представляют как информационные, а информационные входы - как настроечные (следовательно, у мультиплексора 8 ®1 будут три информационных и 8- настроечных входов).

         Пусть функция задана в виде карты Карно (рис.2.15).

При построении УЛМ на карте Карно минимизационные контуры не проводятся.

По карте записывается СHДФ с учетом состояния информационных (настроечных) входов мультиплексора.

Cопоставляя полученную СHДФ с формулой мультиплексора, определяем номера коэффициентов “а”, т.е.

Следовательно, эти коэффициенты равны единице, т.е. D0 = D3 = D5= D6 = 1, а на остальных настроечных входах логические нули, т.е. D1 = D2 = D4 = D7 = 0.

Схема комбинационного устройства, построенного на базе мультиплексора 8-1 и реализующего функцию f (x), приведена на рис. 2.16.

Как следует из рис. 2.16, построение комбинационного устройства на базе мультиплексора сводится к объединению настроечных входов так, чтобы получилось две группы. К одной группе входов, в соответствии с заданной функцией, подают логический “0”, а другой - “1”.

         На базе мультиплексоров можно синтезировать комбинационные устройства, которые могут реализовать функции на большее число переменных, чем количество управляющих входов мультиплексора. Очевидно, и в этом случае, мультиплексор сохраняет свою универсальность, так как часть переменных реализуемой функции непосредственно подается на входы Х1 . . . Хm мультиплексора (количество переменных, непосредственно подаваемых на управляющие входы мультиплексора равно m).

         Синтез комбинационного устройства на мультиплексоре, реализующего функцию с числом переменных больше, чем число управляющих входов мультиплексора. Часто использование мультиплексора при синтезе КУ существенно упрощает этот процесс и схему цифрового автомата.

         В общем случае, когда требуется синтезировать КУ, реализующее функцию N аргументов на мультиплексоре с M управляющими входами и 2М информационными входами, М младших переменных из набора Х1, Х2, . . . .

ХN следует подать на управляющие входы, а информационные сигналы (настроечные) D0, D1, . . . . D2м нужно представить функциями остальных (N - M) переменных, как показано на рис. 2.17. Тогда синтез КУ сводится, по сути дела, к синтезу схемы формирования информационных сигналов, которую можно рассматривать как внутреннее более простое КУ.

Рассмотрим пример синтеза КУ для реализации функции пяти переменных на мультиплексоре с двумя управляющими входами. Тогда “младшие” переменные Х1 и Х2 подаются на управляющие входы Х1и Х2, соответственно. Выходную функцию Y будет определять карта Карно управления информационными входами (рис. 2.18). Каждый информационный сигнал, в свою очередь, является функцией трех переменных: Х3, Х4, Х5. Для каждого информационного сигнала можно составить карту Карно и с её помощью минимизировать логическое выражение функций D0, D1, D2 и D3. По минимизированным логическим выражениям строится схема формирования информационных сигналов (настройки) в любом известном базисе.

         На мультиплексорах с двумя управляющими входами легко можно синтезировать КУ при числе переменных N £ 6. На мультиплексорах с тремя и четырьмя управляющими входами можно синтезировать функции и большего количества переменных. Карты управления информационными входами для этих случаев показаны на рис. 2.18.

         При синтезе КУ на мультиплексорах можно использовать следующий алгоритм действий:

         -составить таблицу истинности КУ;

         -подать на управляющие входы мультиплексора младшие переменные;

         -представить информационные сигналы функциями остальных переменных и составить карту Карно для каждого информационного сигнала;

         - минимизировать логические выражения для сигнала на каждом информационном входе;

-         по логическим выражениям составить схему формирования сигналов, подаваемых на информационные входы мультиплексора.

В задачу синтеза комбинационных устройств

2.1. Основные этапы синтеза комбинационных устройств

В задачу синтеза комбинационных устройств входит построение схемы устройства по заданным условиям его работы и при заданном базисе элементов. Задание комбинационного устройства сводится к заданию тех функций, которые оно должно реализовать. Число функций определяется числом выходов комбинационного устройства.

Процесс синтеза комбинационных устройств состоит из 2-х этапов.

1. Абстрактный синтез

Абстрактный синтез включает:

формирование задачи, словесное описание функций устройства, определение типа устройства; описание устройства на формализованных языках: таблица истинности, карта Карно, аналитическое выражение и т.д.; минимизация булевых функций; построение логической схемы устройства. 2. Схемный синтез

переход в требуемый базис; построение принципиальной схемы; разработка монтажной схемы; изготовление устройства и его испытания. В результате испытаний осуществляются корректировка схемы и подготовка технической документации.

Программируемые логические матричные структуры

2.9. Программируемые логические матричные структуры

Реализация Булевых функций с помощью матричных схем. Матричные схемы представляют собой сетку ортогональных проводников, на местах пересечения которых установлены элементы односторонней проводимости (ЭОП) (диоды, транзисторы). Матричные схемы бывают 2-х и 3-х уровневые. Каждый уровень называется матрицей. Матрица первого уровня называется матрицей М1, матрица второго уровня - М2.

Обычно матрица М1 реализует элементарные конъюнкции и называется матрицей конъюнкций, а матрица М2 - матрицей дизъюнкций, т.к. позволяет реализовать дизъюнкции переменных.

Рассмотрим двухуровневую матричную схему (рис. 2.26).

Рис. 2.26. Функциональная схема матрицы М1:S=3;q=4

Количество входов матрицы М1 равно S, т.е. Х1, Х2, . .. , Xs, количество выходов матрицы М2 равно t, т.е. Y1, Y2, . . , Yt. Буквой Р обозначаются промежуточные проводники, перпендикулярные (ортогональные) проводникам Х и У. Количество ортогональных проводников равно q.

Функциональная схема матрицы М1 представлена на рис. 2.27. Рассматриваемая матрица может реализовать четыре конъюнкции, по числу ортогональных проводников:

Р1 = Х3 Х2

1 ; P2 =

2 X1; P3 =

3 X2; P4 =

3 Х1.

В общем случае, если какие-либо ортогональные проводники не участвуют в реализации конъюнкций, их число может быть меньше q.

Рис. 2.27. Функциональная схема матрицы М1:S=3;q=4

Реализация необходимых конъюнкций осуществляется путем прожига перемычек (включенных последовательно с полупроводниковым диодом), расположенных на местах пересечения ортогональных проводников, не участвующих в образовании конъюнкций.

Следует отметить, что в исходном состоянии на всех пересечениях проводников матрицы М1 имеются соединения, т.е. матрица реализует все конъюнкции переменных, причем в каждую конъюнкцию входят все переменные и с отрицанием, и без. Очевидно, что такие конъюнкции логического смысла не имеют. Для получения необходимых конъюнкций следует прожигать все легкоплавкие перемычки, находящиеся на узлах, не участвующих в конъюнкциях. На схеме (рис. 2.27) рассматриваемой матрицы М1 крестиками обозначены узлы, на которых сохранены перемычки.

Рассмотрим процесс реализации конъюнкции на примере P1 = Х3Х2

1. Действительно, на проводнике P1 будет поддерживаться уровень логической единицы (за счет напряжения источника питания E) только при условии наличия уровня логической "1" на всех трех указанных пересечениях. Очевидно, что на верхнем (по схеме) пересечении уровень "1" будет иметь место только при условии подачи на вход матрицы уровня логического "0", т.к. сигнал Х1 "попадает" на это пересечение через инвертор. Появление "0" хотя бы на одном из входов Х3 или Х2 приводит к "исчезновению" логической "1" на проводе P1, т.к. все напряжение питания Е будет падать на ограничительном сопротивлении R и на выходе Р1 появится "0".

Схема матрицы дизъюнкции М2 содержит сопротивления нагрузки и транзисторные ключевые соединители (на местах пересечений ортогональных проводников). На рис. 2.28 приведена схема матрицы М2 для двух выходов ( количество проводников Р одинаково для М1 и М2 и в данном примере q = 4).

Рис. 2.28. Матрица дизъюнкций М2

Матрица М2, приведенная на рис.1, реализует две дизъюнкции:

Объем информации, который можно записать в матричную схему, определяется как информационная площадь матриц, вернее суммой Sm1 и Sm2.

Sm = Sm1 +Sm2 = 2Sq + qt.

На практике часто встречаются схемы, состоящие из матриц М2 и дешифратора (полного). Такие схемы обычно называют постоянными запоминающими устройствами (ПЗУ). ПЗУ - это элемент (устройство) памяти, позволяющий хранить записанную в нем информацию, и после выключения напряжения источника питания. По способу записи ПЗУ подразделяются на масочные, программируемые и репрограммируемые. Масочные ПЗУ программируются заводом изготовителем с помощью специальных масок, т.е. соединения на местах пересечения ортогональных проводников заложены в технологию производства ПЗУ.

Программируемые ПЗУ (ППЗУ). ППЗУ выпускаются заводом-изготовителем в "чистом виде", т.е. по всем адресам записаны"0". Программирование ППЗУ осуществляется пользователем ППЗУ на специальной установке, называемой программатором. В ППЗУ можно записать (его программировать) информацию только один раз. Изменить записанную информацию или исправить ее нельзя. ППЗУ нашли широкое применение в ЭВМ для хранения запускающих программ. Они обладают большим быстродействием, чем репрограммируемые ПЗУ (РПЗУ).

Репрограммируемые ПЗУ позволяют, при необходимости, перепрограммировать ПЗУ, т.е. стереть ранее записанную информацию и записать новую.

По способу стирания ранее записанной информации РПЗУ бывают с ультрафиолетовым (ультрафиолетовыми лучами) и электрическим стиранием. РПЗУ позволяют десятки (некоторые до 1000) раз перепрограммировать и сохранять записанную информацию десятки и сотни тысяч часов. Быстродействие РПЗУ несколько хуже быстродействия ППЗУ.

Независимо от типа и способа стирания ПЗУ имеют структуру, приведенную на рис. 2.29.

Рис.2.29. Структурная схема постоянного запоминающего устройства

Структурная схема ПЗУ содержит дешифратор на S входов и 2S -выходов, а также матрицу М2.

Информационная емкость ПЗУ определяется как Sпзу = 2S, где S- количество входов X. В этом определении емкости (объема) памяти не учтено количество выходов Y(t). Обычно число t бывает 4, 8, и 16 (полубайтовая, байтовая и двухбайтовая организация памяти). "Битовая" емкость ПЗУ определяется как

Sпзу (бит) = 2S t (бит).

Промышленностью выпускаются ПЗУ с объемом памяти (информационной емкостью) на 2 кбайт, 4 кбайт,16 кбайт,32 кбайт и т.д., где к=1024; 1байт=8бит.

На функциональных и принципиальных схемах РПЗУ с ультрафиолетовым стиранием изображается так, как показано на рис. 2.30.

Рис. 2.30. Схемное обозначение РПЗУ К573РФ2, К573РФ5 с ультрафиолетовым стиранием:

А - адресные входы; D – информационные выходы. Uce – вход подачи напряжения записи (в режиме хранения на этот вход подается Ucc); Ucc – вывод для подачи напряжения питания. СЕ и ОЕ –входы управления состоянием выводов, если СЕ=ОЕ=1, входы D имеют высокоимпедансное состояние. При СЕ=ОЕ=0 вывод информации разрешен.

Микросхема РПЗУ К573РФ2 (РФ5) имеет одиннадцатиразрядный дешифратор, выходы которого соединены с восьмиразрядной матрицей М2. В процессе записи выходные элементы РПЗУ находятся в режиме приема информации через выводы D0 . . . D7 (на входе “ОЕ“ уровень “1”). В режиме считывания записанной информации выводы “Uce” и “Ucc” объединяются, и на них подается напряжение питания +5В.

Схема полусумматора.

Сумматор. В отличие от полусумматора должен воспринимать 3 входных сигнала: 2 слагаемых и сигнал переноса с предыдущего разряда.

Сумматором называется операционный узел ЭВМ, выполняющий операцию арифметического сложения двух чисел.

Чтобы понять сущность работы комбинационного сумматора, рассмотрим примеры суммирования двух одноразрядных двоичных чисел:

Из приведенных примеров (1 - 4) видно, что если отсутствует перенос из младшего разряда, то перенос в старший разряд может быть только в одном случае, когда оба числа равны единице. Если же имеется перенос из младшего разряда, то перенос в старший разряд будет всегда, кроме одного случая, когда оба слагаемых равны нулю.

Составим таблицу функционирования:

ai	bi	Сi	Si	Сi+1
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Схема сумматора может быть реализована на двух полусумматорах, соединенных как указано на схеме рис. 2.22. В этой схеме выделим промежуточные сигналы Pi, gi, ri. Введем эти сигналы в новую таблицу функционирования. Соответствие работы этой схемы (рис. 2.22) и таблицы фунционирования можно проверить перебором всех возможных вариантов.

Рис. 2.22. Схема полного сумматора

это логическое устройство, выполняющее преобразование

2.5. Шифраторы

Шифратор - это логическое устройство, выполняющее преобразование позиционного кода в n разрядный двоичный код. Таким образом, шифратор - это комбинационное устройство, реализующее обратную дешифратору функцию.

Пример шифратора для трех переменных.

Таблица состояния шифратора:

Схема шифратора семиразрядного позиционного кода в трехразрядный двоичный код приведена на рис. 2.12.

Синтез комбинационного устройства-преобразователя кода

2.3. Синтез комбинационного устройства-преобразователя кода

Синтез комбинационного устройства рассмотрим на примере реализации преобразователя кода для семисегментных индикаторов. Будем считать, что светодиодные семисегментные индикаторы выполнены с общим катодом, т.е. сегменты высвечиваются при подаче на них уровня логической единицы. Преобразователь кода представим в виде дешифратора с семью выходами (количество выходов КУ равно количеству реализуемых функций). Схема соединения выводов преобразователя к сегментам индикатора приведена на рис. 2.5. Обозначение сегментов индикатора стандартное и соответствует общепринятым

нормам. В данном случае будем считать, что сегменты будут высвечиваться при подаче на них уровня логической “1”.

Пусть обозначения функций соответствуют именам сегментов, тогда таблица состояния функций будет выглядеть так

Для зажигания цифры 1 необходимо подать уровни логической “1” на сегменты “b” и “c” и т.д. Преобразователь предназначен для индикации цифр десятичной системы счисления, и поэтому значения функций для наборов переменных, начиная с номера 10, для индикатора безразличны. Безразличные значения функций обозначены знаком ~ (тильда).

После заполнения таблицы состояния устройства составляются аналитические выражения (СНДФ) для каждой функции и строятся карты Карно, предназначенные для минимизации этих функций. Карты Карно можно заполнять и без записи СНДФ, что сократит количество действий разработчика при синтезе устройства. Очевидно, что без минимизации функции преобразователя получились бы весьма громоздкими, т.к. каждая содержала бы по девять минтермов, состоящих из четырех переменных. Порядок составления карт Карно и получения минимальных НДФ роли не играют. Для удобства с точки зрения последовательности изложения алгоритма действий, минимизацию начнем с функции а (рис.2.6), реализующей индикацию цифры 0.

Для функции b карта Карно представлена на рис.2.7. Она содержит три контура, следовательно, МДФ будет содержать всего три простых конъюнкции.

Карта Карно для функции “c” представлена на рис.2.8. Она содержит четыре контура, следовательно, функция будет содержать тоже четыре минтерма.

Аналогично строятся карты Карно и записываются минимальные ДФ и для других функций. После получения всех МДФ производят выбор требуемого базиса логических элементов и составляют принципиальную схему. Многие фрагменты отдельных функций могут быть использованы при реализации общих для этих функций операций. В общем случае, принципиальную схему преобразователя кода можно построить на базе элементов И-ИЛИ-НЕ.

это логическая цепь, которая вырабатывает

2.8. Синтез комбинационных сумматоров

Полусумматор это логическая цепь, которая вырабатывает сигналы суммы (S) и переноса (С) при сложении двух двоичных чисел а и в.

Составим таблицу функционирования.

а	в	S	C
0	0	0	0
1	0	1	0
0	1	1	0
1	1	0	1

Из таблицы получим:

. – сигнал суммы;

- сигнал переноса.

Эти выражения упрощению не поддаются.

Приведем к виду, удобному для реализации на элементах ИЛИ-НЕ.

.

исходя из полученных формул составим схему полусумматора (рис. 2.20, а):

Рис.2.20. Схема полусумматора

Поскольку полусумматор имеет широкое применение и его выпускают в виде отдельной микросхемы, он имеет собственное обозначение (рис. 2.20 б).

Составляя дизъюнктивную нормальную форму для полусумматора, мы получили следующие булевы функции:

Следовательно, перенос происходит с помощью функции И, а выработка сигнала суммы (функции неравнозначности) производится элементом ИСКЛЮЧАЮЩЕЕ – ИЛИ. На рис.2.21 показана схема полусумматора, составленная из этих элементов.

Составим логическую цепь трехвходовой пороговой

2.7. Синтез пороговой ячейки

Пороговая ячейка. Составим логическую цепь трехвходовой пороговой ячейки, сигнал на выходе которой будет равен 1; когда на ее входах присутствует не менее двух единиц.

1. Составим таблицу функционирования.

	X1	X2	X3	F
1	0	0	0	0
2	0	0	1	0
3	0	1	0	0
4	0	1	1	1
5	1	0	0	0
6	1	0	1	1
7	1	1	0	1
8	1	1	1	1

2. Для составления логической функции необходимо составить сумму конъюнкций (произведений) всех логических переменных, соответствующих тем строкам, где логическая функция равна 1, причем в конъюнкциях переменная берется без инверсии, если она равна 1, и с инверсией в противном случае:

3. Минимизация полученного выражения. Применим для членов 3 и 4 закон склеивания.

Умножим последнее слагаемое на (1+Х3) (это не изменит общее выражение) и повторим предыдущую процедуру.

Вновь умножим третье слагаемое на (1+Х3):

Применим для слагаемых 3 и 4 закон поглощения. Получим

- это и есть минимизированная функция.

4. Приведем функцию к виду, удобному для реализации на элементах И-НЕ:

.

Применим правило Моргана: Y =

Это выражение можно реализовать в базисе И-НЕ.

Исходя из полученного выражения составим схему (рис.2.19)

Рис. 2.19. Схема пороговой ячейки

Сумматоры с параллельным переносом

Чтобы уменьшить время операции сложения многоразрядных чисел можно использовать схемы параллельного переноса (Carry look-ahead). При этом все сигналы переноса вычисляются непосредственно по значениям входных переменных.

Согласно таблице переключений, в общем случае для сигнала переноса любого i-го разряда справедливо соотношение:

. (1)

Величины gi, ri вычисляются в качестве промежуточных результатов и в полном сумматоре. Следовательно, их получение не требует дополнительных затрат. Смысл этих величин объясняется совсем просто. Сигнал gi вырабатывается тогда, когда в данном разряде перенос происходит из-за комбинации входных переменных ai,bi. Поэтому его называют функцией генерации переноса. Сигнал Pi показывает, передается ли полученный в младшем разряде сигнал переноса Ci дальше. Поэтому он называется функцией распространения переноса.

Пользуясь выражением (1), можно вывести следующие формулы для вычисления сигналов переноса:

(2)

Очевидно, что хотя полученные выражения достаточно сложные, время формирования сигнала переноса в любой разрад с помощью вспомогательных функций определяется только времением здержки распространения сигнала на двух элементах. Эти функции реализуются специальным комбинационным устройством – схемой ускоренного переноса.

Схема сумматора с параллельным переносом приведена на рис. 2.24, а. На рис. 2.24, б изображена схема устройства параллельного переноса в группе из четырех разрядов. Эта схема реализует систему уравнений (2).

Рис. 2.24. Схема сумматора с параллельным переносом

Синтезируйте схему преобразователя кода для

         2.1. Объясните причины возникновения гонок в комбинационных устройствах.
         2.2. Синтезируйте схему преобразователя кода для 9 и 13 сегментных индикаторов.
         2.3. Можно ли построить полный дешифратор на элементах базиса ИЛИ-НЕ? Составьте аналитическое выражение (функции), описывающее работу дешифратора в базисе И-НЕ.
         2.4. Синтезируйте схему мультиплексора 2-1, и на базе синтезированного мультиплексора постройте схему сумматора по модулю два (исключительное ИЛИ).
         2.5. Определите информационную площадь (SПЛМ) ПЛМ, ПЗУ при произвольных значениях количества информационных входов. Докажите, что SПЗУ > SПЛМ.
         2.6. Нарисуйте схему фрагмента КУ, приведенного на рис. 2.32, в базисе ИЛИ-НЕ.
         2.7. Нарисуйте схему четырёхразрядного полного дешифратора на базе дешифраторов 2-4. Базовые дешифраторы имеют один дополнительный вход стробирования.

D-триггер

В технической литературе D-триггер, управляемый уровнем синхроимпульса, известен также как триггер-защелка.

Пример синтеза D-триггера, управляемого уровнем синхроимпульса из асинхронного одноступенчатого RS-триггера. Для этого D-триггер представляют как совокупность RS-триггера и комбинационного входного устройства, т.е. представляется так, что входными линиями RS-триггера управляет комбинационное устройство (КУ), согласно характеристической формуле D-триггера (см. рис. 3.11, в). Входными переменными КУ являются сигналы Q0 , C, D, а выходными (функциями) - S и R. Если учесть, что сигналы R и S являются для RS-триггера управляющими сигналами, то таблица состояний синтезируемого триггера будет содержать пять столбцов: два столбца - для переменных D-триггера - D и Q0, один - для функции Q (выходной сигнал синтезируемого триггера, он же является выходным сигналом базового RS-триггера) и два столбца - для переменных R и S RS-триггера

Столбцы 1, 2, 3 соответствуют таблице состояний D-триггера, а в столбцы 4, 5 записываются значения сигналов R и S, при подаче которых на входы RS-триггера, последний должен принимать такие же состояния, что и D-триггер. Это обусловлено тем, что RS-триггер является выходным узлом D-триггера.

Из таблицы (рис.3.12, а, первая строка) следует: если триггер находился в состоянии “0” (Q0 =0), чтобы он сохранил это состояние и после поступления очередного синхроимпульса (отметим, что переключение состояния триггера происходит только при наличии синхроимпульса, а каждая строка таблицы состояний соответствует новому синхроимпульсу) на входе S (RS-триггера) необходимо поддерживать уровень “0”, а на входе R - любой уровень, т.к. когда триггер находится в состоянии”0”, он сохраняет это состояние независимо от состояния сигнала R.

Для второй строки таблицы состояний Q0=1, а новое состояние триггера “0” (Q=0), следовательно, необходимо подать на вход R - уровень логической 1 и т.д.

Для каждой строки, где Q0=1, это состояние триггера сохранится независимо от значения сигнала S (т.к. при S=0 - режим хранения, а при S=1 - запись единицы).

После заполнения таблицы состояний, используя карты Карно (рис. 3.12, б и в), записывают логические выражения для функций комбинационного устройства S и R (следует помнить, что эти сигналы являются функциями аргументов Q0 , D и входными переменными для RS-триггера.

По полученным логическим выражениям (см. рис. 3.12, б и в) можно построить схему D-триггера (рис. 3.12, г).

Рассмотренный выше D-триггер синтезирован на базе синхронного RS-триггера. Его можно синтезировать и на базе двухступенчатого, а также - простого, асинхронного RS-триггера. Как уже было отмечено выше, переключение D-триггера происходит только при наличии (поступлении) синхроимпульса. С учетом этого, логические функции S и R можно записать в виде

S = C D;

Схема, реализующая эти функции, содержит два элемента конъюнкции и один инвертор. На рис. 3.13 приведена схема D-триггера, построенного на базе асинхронного RS-триггера.

На рис. 3.14 приведено обозначение D-триггера К1533ТМ2, выпускаемого промышленностью в виде интегральной микросхемы (ИМС).

Обычно, в одном корпусе ИМС содержится два D-триггера, управляемых фронтом. D-триггеры в интегральном исполнении имеют также дополнительные асинхронные входы управления S и R. Функции асинхронных входов не зависят от сигналов синхронизации. Отметим, что асинхронные входы имеют и другие типы триггеров. Поскольку дополнительные входы “предустановка” и “очистка”, с помощью которых триггер может быть установлен в нужное состояние независимо от сигналов на других входах, включая синхронизирующий, работают независимо от синхронизации, их называют асинхронными.

Входы “предустановки” и “очистки” напоминают соответствующие входы S и R обычного несинхронизируемого RS-триггера. При подаче “1” на вход R и “0” на вход S (рис. 3.14) триггер устанавливается в состояние “0”. При подаче “1” на оба эти входа поведение триггера не определено, т.е. комбинация S=1, R=1 является запрещенной. При подаче на эти входы “1” поведение триггера полностью определяется другими входными сигналами и синхросигналом.

Функциональный счетчик В.М. Сапельникова

На этих триггерах собран девятиразрядный резистор сдвига. RS – триггер (элемент 10) применяется для задания режима работы функционального счетчика. С этой же целью используются еще два элемента 3И-НЕ (элементы 11 и 12). Синхронизирующие импульсы поступают от кнопки “СИ” (синхроимпульсы), и для устранения возможного “дребезга” применяются логические схемы 2И-НЕ (элементы 13-14).

Функциональный счетчик позволяет получать различные кодовые последовательности. Линейно - нарастающую кодовую последовательность получаем, когда триггеры регистра сдвига 1-9 последовательно от первого к последнему устанавливаются в состоянии “1”, а затем все одновременно устанавливаются в состояние “0”. Линейно убывающую кодовую последовательность, когда триггеры регистра сдвига последовательно от последнего к первому устанавливаются в состояние “0”, а затем все одновременно устанавливаются в состояние “1”.

Можно получить линейно-нарастающе-убывающую кодовую последовательность. Именно этой кодовой последовательности соответствует основной режим работы, используемый в калибраторе фазы и описываемый таблицей переключений (табл. 3.3).

Рассмотрим этот режим работы. В исходном состоянии триггеры 1-9 находятся в состоянии “0”, триггер 10 в состоянии “1”. На третьи входы элементов ЗИ-НЕ (элементы 11-12) устанавливается логический “0” переключателями S1 и S2. При этом на асинхронные R и S входы триггеров регистра сдвига поступает “1”.

Первый синхронизирующий импульс устанавливает триггер 1 в состояние “1”, не изменяя состояния других триггеров. После этого второй JK – триггер регистра сдвига подготовлен к записи “1” по третьему J–входу. Второй синхронизирующий импульс устанавливает триггер 2 в состояние «1» и по третьему J-входу подготавливает следующий триггер к приему “1”. Аналогично с приходом каждого последующего синхроимпульса и в соответствии с табл. 3.3 происходит переключение в “1” триггеров регистра сдвига до прихода девятого импульса. С приходом девятого синхроимпульса последний JK- триггер регистра сдвига переходит в “1”.При этом RS- триггер (элемент 10) переходит в состояние “0”. Переход RS-триггера в состояние “0” подготавливает все триггеры регистра сдвига к приему “0”. Так у девятого JK–триггера на два J-входа теперь поступает “0”, и на все три К - входа поступает “1” с выходов вспомогательного RS-триггера. Таким образом, последний JK-триггер готов к приему “0”. Остальные же восемь JK-триггеров будут последовательно готовиться к приему «0» путем подачи на первые К - входы недостающей “1” при переходе в состояние “0” находящегося справа от него JK-триггера. В этом случае на инверсном выходе JK-триггера появляется логическая “1”.

3.8. Функциональный счетчик В.М. Сапельникова

При создании калибраторов фазы необходимо формировать два синусоидальных сигнала. Каждый из них можно получить с помощью управляемых ЦАП в виде ступенчатой функции – квазисинусоидальный сигнал (рис. 3.43). Причем, если ступеньки формировать через 100 и величина ступеньки обеспечит точное значение синусоидальной зависимости для этого значения фазы, то первая из высших гармоник будет иметь высокий порядок. Это обстоятельство облегчает выделение основной гармоники и снижает требования к фильтрам, применяемым в калибраторах фазы. Используя специально подобранные резисторы в соответствии с величиной ступеньки, можно при формировании квазисинусоидального сигнала каждый раз добавлять всего один резистор.

Рис. 3.43.

Управление таким ЦАП удобно производить с помощью функционального счетчика который должен иметь девять разрядов Q1 и таблицу переключений (табл. 3.3), определяющую код работы функционального счетчика. Цикл работы составляет 18 тактов и требует 18 синхроимпульсов С.

Схема функционального счетчика приведена на рис. 3.44. Счетчик собран на девяти JK – триггерах (элементы 1 - 9) типа К155ТВ1, имеющих по три J – входа и три К – входа, объединенных по И. Триггеры имеют асинхронные установочные R и S входы.

Электронные счетчики и делители частоты

3.7. Электронные счетчики и делители частоты

На базе счетных триггеров можно построить цифровое устройство, получившее название электронного счетчика. Электронные счетчики ( далее, просто счетчики) позволяют вести подсчет электрических импульсов, количество которых (поступивших на вход счетчика) представляется, обычно, в параллельном коде. Счетчики могут отличаться модулем счета и типом счетной последовательности, которая, в частности, может быть двоичной, двоично-десятичной, в коде Грея и т.п. Цифровые последовательностные устройства, выполненные по схеме счетчика, но имеющие один счетный вход и один выход называются делителями частоты. Таким образом, любой счетчик может служить в качестве делителя частоты, если используется информация только одного из его выходов. Так как счетчики и делители имеют единую структуру, основное внимание будет уделено синтезу счетчиков.

Счетчики и делители подразделяются на асинхронные и синхронные. У синхронных счетчиков все разрядные триггеры синхронизируются параллельно одними и теми же синхроимпульсами, поступающими из источника этих импульсов. Асинхронные счетчики имеют последовательную синхронизацию, т.е. каждый последующий разрядный триггер синхронизируется выходными импульсами триггера предыдущего разряда. Асинхронные счетчики иногда называют последовательными, а синхронные счетчики - параллельными.

Синхронные счетчики, в свою очередь, подразделяются на параллельно-синхронные и последовательно-синхронные. Параллельные счетчики имеют более высокую скорость счета, чем асинхронные.

Счетчики, независимо от способа синхронизации, подразделяются на счетчики прямого счета (суммирующие) и на счетчики обратного счета (вычитающие). В интегральном исполнении выпускаются также реверсивные счетчики, в которых имеется специальный вход для переключения режима работы, т.е. направления счета. Многие типы счетчиков, выпускаемые промышленностью в интегральном исполнении, имеют дополнительные входы предустановки, позволяющие использовать эти счетчики в режиме регистра памяти.

Рис. 3.33. Схема а), таблица состояний триггеров б) и временные диаграммы, поясняющие работу в) последовательного четырехразрядного счетчика на

JK - триггерах

Временные диаграммы, поясняющие работу асинхронного суммирующего счетчика приведены на рис. 3.33, в.

Счетчики обратного счета (вычитающие счетчики). На рис. 3.34 приведена схема асинхронного трехразрядного двоичного вычитающего счетчика, построенного на базе D-триггеров. Отметим, что условия для изменения состояний триггеров вычитающих счетчиков аналогичны условиям для суммирующих счетчиков с той лишь разницей, что они должны “опираться” на значения инверсных, а не прямых выходов триггеров. Следовательно, рассмотренный выше счетчик можно превратить в вычитающий, просто переключив входы “С” триггеров с выходов Q на выходы

. Когда в качестве разрядных триггеров используются D-триггеры, синхронизируемые передним фронтом синхроимпульсов, для получения вычитающего счетчика (асинхронного) входы “С” последующих тригеров соединяются с прямыми выходами предыдущих, также как в счетчике прямого счета, построенного на JK-триггерах.

Работа вычитающего счетчика на D-триггерах наглядно иллюстрирована на рис. 3.34, (б). Из рис. 3.34 следует, что после нулевого состояния всех триггеров, с приходом первого синхроимпульса они устанавливаются в состояние “1”. Поступление второго синхроимпульса приводит к уменьшению этого числа на одну единицу и т.д. После поступления восьмого импульса, снова, все триггеры обнуляются и цикл счета повторяется, что соответствует модулю М=8.

В некоторых случаях необходимо, чтобы счетчик мог работать как в прямом, так и в обратном направлении счета. Такие счетчики называются реверсивными. Реверсивные счетчики могут быть как асинхронного, так и синхронного типа. Они строятся путем применения логических коммутаторов (мультиплексоров) в цепях связи между триггерами. Так, например, асинхронный реверсивный двоичный счетчик можно построить, если обеспечить подачу сигналов с прямого (при суммировании) или с инверсного (при вычитании) выхода пре-дыдущего JK- или Т-триггера на счетный вход последующего.

В случае, когда реверсивный счетчик строится на базе D-триггеров, управляемых передним фронтом, для получения режима прямого счета следует соединить инверсный выход предыдущего с счетным входом последующего триггера.

Все рассмотренные типы счетчиков могут быть использованы в цифровых устройствах “умеренного” быстродействия, когда частота следования синхроимпульсов не превышает критического значения, при котором время задержки установки триггеров последних (старших) разрядов счетчика становится соизмеримым с длительностью периода входных тактовых импульсов. В связи с этим, асинхронные счетчики строятся на относительно небольшое количество разрядов, так как при большем количестве разрядов выходные сигналы триггеров старших разрядов появляются позднее, чем управляющие фронты синхроимпульсов (поступающих на вход первого триггера) .

Параллельные счетчики (синхронные счетчики). Как было уже сказано выше, параллельные счетчики бывают двух типов: синхронные параллельные и синхронные последовательные.

Синхронный последовательный счетчик. По способу подачи синхроимпульсов такие счетчики параллельные, т.е. синхроимпульсы поступают на все триггеры счетчика параллельно, а по способу управления (подачи управляющих импульсов) - последовательные. Схема синхронного последовательного счетчика, реализованного на JK-триг-герах, приведена на рис. 3.35.

Синхронный последовательный счетчик обладает повышенным быстродействием, однако, за счет последовательного формирования управляющих уровней, на входы “J” и “К” счетных триггеров, быстродействие несколько уменьшается. От этого недостатка лишены параллельные синхронные счетчики, в которых формирование управляющих уровней и их подача на соответствующие входы триггеров счетчика осуществляется одновременно, т.е. параллельно. Пример реализации параллельного синхронного счетчика иллюстрирован на рис. 3.36.

Поскольку счетчик имеет одну общую линию синхронизации, состояние триггеров меняется синхронно, т.е.

те триггеры, которые по синхроимпульсу должны изменить свое состояние, делают это одновременно, что существенно повышает быстродействие синхронных счетчиков.

Счетчики с произвольным коэффициентом счета. Принцип построения подобного класса счетных устройств состоит в исключении нескольких состояний обычного двоичного счетчика, являющихся избыточными для счетчиков с коэффициентом пересчета, отличающимися от двоичных. При этом избыточные состояния исключаются с помощью обратных связей внутри счетчика.

Число избыточных состояний для любого счетчика определяется из следующего выражения:

М = 2m - Ксч,

где М - число запрещенных состояний, Ксч - требуемый коэффициент счета; 2m - число устойчивых состояний двоичного счетчика.

Задача синтеза счетчика с произвольным коэффициентом счета заключается в определении необходимых обратных связей и минимизации их числа. Требуемое количество триггеров определяется из выражения

n= [log2 Ксч],

где [log2 Ксч] - двоичный логарифм заданного коэффициента пересчета Ксч, округленный до ближайшего целого числа.

В каждом отдельном случае приходится применять какие-то конкретные методы получения требуемого коэффициента пересчета. Существует несколько методов получения счетчиков с заданным коэффициентом пересчета Ксч. Один их этих методов заключается в немедленном сбросе в “0” счетчика, установившегося в комбинацию, соответствующему числу Ксч. Его называют также методом автосброса. Рассмотрим пример реализации счетчика с Ксч=10 методом автосброса. Очевидно, что “сбрасывая” двоичный четырехразрядный счетчик на нуль каждый раз, когда он будет принимать состояние 1010, можно обеспечить”возврат” счетчика в исходное состояние после каждых десяти импульсов. Подобный прием удобно применять при использовании счетчиков в интегральном исполнении, имеющих ячейки конъюнкции (И) на входах установки в нуль, как это сделано в микросхеме К1533ИЕ5. В данном примере (рис. 3.37) организованы соединения, обеспечивающие коэффициент пересчета Ксч =10.

Как следует из рис. 3.37, роль ячейки, выявляющей факт достижения кодовой комбинации 1010 на выходах счетчика, играет ячейка И, уже имеющаяся на входе сброса ИМС К1533ИЕ5. В таблице 3.1 поясняются конфигурации соединений для получения различных коэффициентов пересчета с помощью счетчика К1533ИЕ5. Наиболее очевидные варианты получения коэффициентов (2, 4, 8, 16 ) в таблице не указаны. В графе “Соединения” таблицы указано, какие выводы микросхемы должны быть соединены между собой: например, указание 1-12 означает, что нужно соединить вывод 1 с выводом 12. В строках “Ввод” и “Выход” таблицы указаны номера выводов микросхемы, на которые следует подавать входные импульсы и с которых надлежит снимать выходные, соответственно. Следует отметить, что ИМС К1533ИЕ5 состоит из четырех счетных триггеров, один из которых имеет раздельные выводы входа и выхода, а остальные три триггера соединены последовательно по схеме асинхронного счетчика.

Синтез счетчика с произвольным коэффициентом счета. Один из методов проектирования счетчиков с заданным коэффициентом счета заключается в построении таблицы переходов, в первых столбцах которых будут отражены текущие состояния триггеров счетчика, а в последующих - следующие за ними состояния. Анализ таблицы позволяет установить те переходы, которые должны быть “сделаны” триггерами, входящими в состав счетчика. Затем с помощью управляющей таблицы соответствующего триггера находятся значения логических функций на управляющих входах триггеров, позволяющие осуществить эти переходы.

Рассмотрим пример синтеза синхронного двоично-десятичного счетчика на базе JK-триггеров. На рис. 3.38 показан граф, поясняющий последовательность переходов десятичного счетчика, в таблице 3.2 - таблица переходов.

В правой части таблицы 3.2 приведены значения входных сигналов четырех триггеров. Для поиска этих значений должны быть проанализированы реализованные переходы, а затем с помощью управляющей таблицы (см.

рис. 3.15, а) определены соответствующие значения “J” и “K” входов триггеров.

На рис.3. 39 приведены карты Карно для логических функций, которым должны соответствовать сигналы, присутствующие на управ-ляющих входах триггеров ( нулевые значения функций в клетки карты Карно не записаны).

После упрощения с помощью карт Карно полученные логические выражения, используемые для управления входами “J” и “К”, выглядят

J4 = Q1 Q2 Q3 ; K4 = Q1

J3 = Q1 Q2; K3 = Q1 Q2;

J2 =

K2 = Q1

Просмотр столбцов J1 и К1 в табл. 3.2 показывает, что все значения либо “~“, либо “1”. Так как безразличные состояния могут также участвовать в процессе упрощения, то все клетки карты Карно для J1 и К1 оказываются заполненными символами “~“, “1” и “a“. Следовательно,

J1 = K1 = 1

На рис. 3.40 показана схема двоично-десятичного синхронного счетчика.

Если счетчик из-за какой-либо неисправности окажется в одном из запрещенных (неиспользуемых) состояний, то его работа может быть прервана специальным сигналом и также может быть подан сигнал тревоги о неисправности в схеме счетчика. Обнаружить это позволяет схема, реализующая выражение, описывающее функцию неиспользуемых состояний

fн = Q2 Q4 + Q3 Q4 .

На рис. 3.41 показано, как эта схема используется для формирования цепи аварийной сигнализации и генерации блокирующего сигнала синхронизации.

Выражение , описывающее блокирующий сигнал синхронизации, имеет вид

Следовательно, когда fн = 1, то С’ = 0, и синхроимпульсы будут отсутствовать до тех пор, пока счетчик не выйдет из запрещенного состояния. Из схемы формирования блокирующего сигнала синхронизации следует, что логика её функционирования ориентирована на то, чтобы исключить возможность появления неиспользуемых комбинаций выходных сигналов. Действительно, в коде числа двоично-десятичного счетчика отсутствуют комбинации 0110, 0011, следовательно, их появление свидетельствует о неиспраности системы.

Временные диаграммы счетчика (рис. 3.40), заданного графом переходов (рис. 3.38) и таблицей переходов 3.2, приведены на рис. 3.42.

Из рис. 3.42 следует, что все изменения состояний триггеров происходят во время формирования заднего фронта положительного импульса синхронизации. На временных диаграммах выходов Q1 . . . Q4 присутствуют двоичные цифры, характеризующие текущее состояние счетчика.

JK-триггер

3.4. JK-триггер

Среди триггеров особое место занимают JK-триггеры, имеющие более широкие функциональные возможности.

Упрощенная таблица (таблица управления) состояний JK-триг-гера содержит четыре строки (рис. 3.15, а).

Из таблицы состояний видно, что для первых трех строк (наборов переменных) входы J и K играют роль входов S и R RS - триггера. Однако, для четвертого набора переменных, когда J=K=1 состояние триггера сильно отличается от состояния RS-триггера. Для RS-триггера - это запрещенная комбинация входных переменных, а в JK-триггере меняется (инвертируется) предыдущее состояние. JK-триггер можно синтезировать (построить) на базе двухступенчатого RS-триггера, для чего следует представить функциональную схему JK-триггера как совокупность КУ и синхронного RS-триггера (рис. 3.15, б).

Для получения логических выражений (характеристических уравнений) функций R и S комбинационного устройства необходимо построить совмещенную таблицу состояний JK и RS - триггеров (рис. 3.16, а).

Из полученных выражений для S и R (рис. 3.16, б) следует, что для построения JK-триггера из двухступенчатого RS-триггера потребуется два элемента конъюнкции (на два входа каждый). Схема, полученная путем синтеза JK-триггера, приведена на рис. 3.17, а. Обозначение JK-триггера на функциональных схемах приведено на рис. 3.17, б.

Рис. 3.17. Синтезируемая схема а) и графическое обозначение б) JK - триггера

Выпускаемые промышленностью ИМС JK-триггеры могут иметь несколько входов (до трех) J и такое же количество входов K, объединенных схемами конъюнкций (рис. 3.18).

Рис. 3.18. Схемное обозначение ИМС JK – триггера, выпускаемого промышленностью

Как следует из рис. 3.18, выпускаемые промышленностью JK-триггеры в виде интегральных микросхем также имеют асинхронные входы установки “0” и “1”(R и S входы, соответственно).

Понятие последовательностного автомата

3.1. Понятие последовательностного автомата

Последовательностные цифровые устройства часто называют последовательностными схемами, последовательностными автоматами, дискретными автоматами с памятью, многотактными автоматами.

Кроме комбинационных устройств, рассмотренных в предыдущей главе, существует класс цифровых устройств, в которых при одинаковых воздействиях на входе, на выходе автомата могут возникать различные выходные состояния. Состояние выхода такого устройства зависит не только от того, какие сигналы присутствуют на его входах в данный момент времени, но и от того, какие последовательности сигналов поступали на входы устройства в предшествующие моменты времени, т.е. как говорят, автомат помнит свою предысторию и хранит ее в памяти. Поэтому такие устройства называют последовательностными или многотактными автоматами.

Для описания последовательностного автомата с памятью, помимо состояний входов X(t) и выходов Y(t), необходимо также знать состояние памяти автомата, как говорят, его внутреннее состояние S(t).

В общем виде, последовательностный автомат рассматривается состоящим из двух частей: комбинационного устройства (КУ) и памяти, состоящей из элементов памяти (ЭП) (рис. 3.1).

В качестве элементов памяти могут быть применены как однобитовые элементы памяти (различные типы триггеров), так и многобитовые (многоразрядные) цепочки триггеров.

Функционирование (т.е. изменение состояния устройства) многотактного автомата происходит в дискретные моменты времени, ход которого обозначается натуральными числами t = 1, 2, 3 и т.д. В каждый момент дискретного времени t автомат находится в определенном состоянии S(t), воспринимает через входы соответствующую данному моменту комбинацию входных переменных X(t), выдает на выходах некоторую функцию выхода Y(t), определяемую как

Y(t) = f (S(t),X(t)),

и переключается в новое состояние S(t+1), которое определяется функцией переходов j как

S(t+1)= j ( S(t),X(t)).

Закон функционирования последовательностных автоматов может задаваться в виде уравнений, таблиц и графов. Под законом функционирования понимается совокупность правил, описывающих последовательность переключения состояний автомата и последовательность выходных сигналов в зависимости от последовательности поступления входных сигналов.

ЭП часто реализуется на основе бистабильных ячеек (БЯ). ЭП бывают: динамические, статические и квазидинамические. Наибольшее распространение получили первых два вида: статические и динамические. Статические ЭП реа- лизуются на БЯ. Динамические ЭП строятся, используя свойство хранения заряда между затвором и истоком полевых транзисторов МДП структуры.

БЯ - является простейшим типом триггера, реализованного с помощью элементов базиса И - НЕ или ИЛИ - НЕ с соответствующими обратными связями и позволяет хранить один бит цифровой информации (бит - единица цифровой информации, соответствующая одной логической “1” или логическому “0”).

Триггер - это последовательностная схема с двумя состояниями, каждое из которых при опреленных условиях на входах поддерживается постоянным (т.е. стабильным). Каждому из этих состояний ставится в соответствие логическое значение, которое “хранит” триггер (если на выходе триггера высокий уровень напряжения - “1” и “0” - в противном случае). Таким образом, в последовательностной схеме для представления значений каждой переменной, которую нужно хранить для использования в настоящем или в будущем, следует использовать отдельный триггер. Совокупное состояние последовательностной схемы, запоминающее устройство которой реализовано на триггерах, представляет собой просто комбинацию состояний этих триггеров.

Вообще говоря, у триггера должна быть по крайней мере одна выходная линия, представляющая логическое значение, соответствующее состоянию триггера. Когда на выходной линии логическая 1, говорят, что триггер установлен, в противном случае говорят, что триггер сброшен. Триггер имеет несколько входных линий, сигналы на которых (вместе с текущим состоянием триггера) определяют следующее состояние триггера. От функций входных линий зависит тип триггера.

Простейшим триггером является RS - триггер. RS - триггер имеет два входа и два выхода. Входы и выходы триггера имеют свои обозначения. Один из входов триггера называется установочным входом и обозначается буквой S (от английского set - установить), а другой - входом сброса и обозначается буквой R ( от reset - сбросить). Триггер (рис. 3.2) имеет два симметричных выхода. На одном выходе (условно называемом прямым выходом) сигнал представляется без отрицания (выход Q), а на другом - с отрицанием (`Q - инверсный выход).

   По способу подачи переключающих сигналов (в зависимости от комбинации входных сигналов) триггеры делятся на RS, MS, D, JK, T - триггеры.

Рис. .3.2. Графическое обозначение

RS - триггера

Триггеры бывают переключающимися уровнем и фронтом тактирующего сигнала ( импульса ). Несмотря на большое разнообразие триггеров, практически все триггеры строятся на базе RS -триггеров.

Регистры

3.6. Регистры

Наиболее распространенным узлом цифровой техники и устройств автоматики являются регистры. Регистры строятся на базе синхронных одно- и двухступенчатых RS и D-триггеров. Регистры могут быть реализованы также на базе JK -триггеров. По способу приема и выдачи информации регистры делятся на следующие группы: с параллельным приемом и выдачей (рис. 3.25, а); с последовательным приемом и выдачей (рис. 3.25, б); с последовательным приемом и параллельной выдачей (рис. 3.25, в); с параллельным приемом и последовательной выдачей (рис. 3.25, г); комбинированные, с различными способами приема и выдачи (рис. 3.25, д) и реверсивные.

Регистры хранения (пямяти). Регистры с параллельным приемом и выдачей информации служат для хранения информации и называются регистрами памяти или хранения. Изменение хранящейся информации в регистре памяти (запись новой информации) осуществляется после установки на входах D0 . . . Dm новой цифровой комбинации (информации) при поступлении определен-

ного уровня или фронта синхросигнала (синхроимпульса) С на вход “С” регистра. Количество разрядов записываемой цифровой информации определяется разрядностью регистра, а разрядность регистра, в свою очередь, определяется количеством триггеров, образующих этот регистр. В качестве разрядных триггеров регистра памяти используются синхронизируемые уровнем или фронтом триггеры. Регистры памяти могут быть реализованы на D-триггерах, если информация поступает на входы регистра в виде однофазных сигналов и на RS-триггерах, если информация поступает в виде парафазных сигналов. В некоторых случаях регистры могут иметь вход для установки выходов в состояние “0”. Этот асинхронный вход называют входом R “сброса” триггеров регистра. На рис. 3.26 приведены схемы четырехразрядных регистров памяти на D- и RS-триггерах, синхронизируемых уровнем и фронтом синхроимпульсов (обычно четыре триггера объединены в одном корпусе ИМС).

а)                           б)                                  в)

Рис. 3.26. Регистры хранения, на D – триггерах, синхронизируемых уровнем синроимпульса (а), фронтом (б) и на RS – триггерах, синхронизируемых фронтом (в)

Регистры сдвига. Регистры с последовательным приемом или выдачей информации называются сдвиговыми регистрами или регистрами сдвига. Регистры сдвига могут выполнять функции хранения и преобразования информации. Они могут быть использованы для построения умножителей и делителей чисел двоичной системы счисления, т.к. сдвиг двоичного числа влево на один разряд соответствует умножению его на два, а сдвиг вправо - делению на два. Регистры сдвига широко используются для выполнения различных временных преобразований цифровой информации: последовательное накопление последовательной цифровой информации с последующей одновременной выдачей (преобразование последовательной цифровой информации в параллельный код) или одновременный прием (параллельный прием) информации с последующей последовательной выдачей (преобразование параллельного кода в последовательный). Регистры сдвига могут служить также в качестве элементов задержки сигнала, представленного в цифровой форме. Действительно, регистры с последовательным приемом (вводом) и выводом осуществляют задержку передачи информации на m+1 тактов ( m+1 - число разрядов регистра) машинного времени.          Регистры сдвига обычно реализуются на D-триггерах (рис. 3.27, а) или на RS-триггерах (рис. 3.27, б), где для ввода информации в первый разряд включается инвертор (первый разряд представляет собой D-триггер). Следует отметить, что все регистры сдвига строятся на базе двухступенчатых триггеров или синхронизируемых фронтом синхроимпульса.

Разрядность регистров сдвига, как и у регистров хранения, определяется количеством триггеров, входящих в их состав. На рис. 3.27 приведены схемы четырехразрядных регистров сдвига, реализованных на D- и RS-триггерах, а временные диаграммы, поясняющие работу регистра сдвига, приведены на рис. 3.28.

Вывод параллельной информации из регистра сдвига (см. рис. 3.27, в) осуществляется при подключении всех триггеров регистра к отдельным выводам (на рис. 3.27, а и б эти выводы показаны штриховыми линиями). Как было сказано выше, регистры сдвига синхронизируются фронтом тактирующих импульсов, т.е. запись новой информации в триггеры регистра происходит в течение очень короткого времени - за время длительности фронта синхроимпульса, вернее в момент поступления соответствующего фронта синхроимпульса. Обычно, это “время” значительно меньше времени распространения сигнала, т.е. времени переключения триггера регистра в новое состояние. Работу регистра сдвига рассмотрим на примере схемы, приведенной на рис. 3.27, а.

Можно предположить, что в начале все триггеры регистра находятся в состоянии логического нуля, т.е. Q0=0, Q1=0, Q2=0, Q3=0. Если на входе D-триггера Т1 имеет место логический 0, то поступление синхроимпульсов на входы “С” триггеров не меняет их состояния.

Как следует из рис. 3.27, синхроимпульсы поступают на соответствующие входы всех триггеров регистра одновременно и записывают в них то, что имеет место на их информационных входах. На информационных входах триггеров Т2, Т3, Т4 - уровни логического “0”, т.к. информационные входы последующих триггеров соединены с выходами предыдущих триггеров, находящихся в состоянии логического “0”, а на вход “D” первого триггера, по условию примера, подается “0” из внешнего источника информации. При подаче на вход “D” первого триггера “1”, с приходом первого синхроимпульса, в этот триггер запишется “1”, а в остальные триггеры - “0”, т.к. к моменту поступления фронта синхроимпульса на выходе триггера Т1 “ещё” присутствовал логический “0”.

Таким образом, в триггер Т1 записывается та информация (тот бит), которая была на его входе “D” в момент поступления фронта синхроимпульса и т.д.

При поступлении второго синхроимпульса логическая “1” , с выхода первого триггера, запишется во второй триггер, и в результате происходит сдвиг первоначально записанной “1” с триггера Т1 в триггер Т2, из триггера Т2 в триггер Т3 и т.д. (рис. 3.28). Таким образом, производится последовательный сдвиг поступающей на вход регистра информации (в последовательном коде) на один разряд вправо в каждом такте синхроимпульсов.

         После поступления m синхроимпульсов (на рис. 3.27 и рис. 3.28 m=4) регистр оказывается полностью заполненным разрядами числа, вводимого через последовательный ввод “D”. В течение следующих четырех синхроимпульсов производится последовательный поразрядный вывод из регистра записанного числа, после чего регистр оказывается полностью очищенным (регистр окажется полностью очищенным только при условии подачи на его вход уровня “0” в режиме вывода записанного числа).

Рис. 3.27. Регистры сдвига на D – триггерах а), RS – триггерах б) и комбинированный регистр на D - триггерах

Кольцевые счетчики. На базе регистров сдвига можно построить кольцевые счетчики - счетчики Джонсона. Счетчик Джонсона имеет коэффициент пересчета, вдвое больший числа составляющих его триггеров. В частности, если счетчик состоит из трех триггеров (m=3), то он будет иметь шесть устойчивых состояний. Счетчик Джонсона используется в системах автоматики в качестве распределителей импульсов и т.д.

Таблица состояний счетчика Джонсона (рис. 3.29) содержит 2m (m - количество триггеров в составе регистра) строк и m-столбцов. Количество разрядов счетчика определяется количеством триггеров (рис. 3.29). Рассмотрим схему трехразрядного счетчика Джонсона, выполненного на базе D-триггеров (регистр сдвига реализован на D-триггерах). Для построения кольцевого счетчика достаточно соединить инверсный выход последнего триггера регистра (последнего разряда) с входом “D” (с входом, предназначенным для ввода последовательной информации) первого триггера.

Рис. 3.29. Таблица состояний а) и схема б) счетчика Джонсона на трехразрядном регистре сдвига

Предположим, что вначале все триггеры находятся в состоянии “0”, т.е. Q0= Q1=Q2=0. При этом на входе “D” первого триггера присутствует уровень “1”, т.к

=1. Первым синхроимпульсом в триггер Т1 запишется “1”, вторым - единица запишется в первый триггер, из первого - во второй и т.д. до тех пор, пока на всех выходах регистра не будет “1”. После заполнения регистра единицами, на инверсном выходе триггера Т3 появится

=0 и четвертым синхроимпульсом в Т1 запишется логический “0” (рис. 3.29, б).

После поступления последующих трех синхроимпульсов регистр обнуляется и на его вход “D” снова подается уровень “1”. Таким образом, цикл повторения состояния кольцевого счетчика состоит из шести тактов синхросигнала. Как видим, при работе в начале от первого триггера до последнего триггера распространяется “волна единиц”, а затем “волна нулей”. Код, в котором работает счетчик Джонсона, называют кодом Либау-Крейга.

Генераторы чисел. На базе кольцевых счетчиков можно реализовать генераторы различных двоичных чисел. Вывод генерируемых чисел можно осуществлять как в параллельном, так и в последовательном коде.

В качестве примера рассмотрим работу трехразрядного (очевид-но, что количество разрядов может быть и более трех) генератора чисел, реализованного на базе D-триггеров. Генератор чисел представим как совокупность трехразрядного регистра сдвига и комбинационного устройства КУ, выходной сигнал которого служит “источником” информации для регистра сдвига (рис. 3.30). Входными переменными КУ являются выходные сигналы разрядных триггеров регистра сдвига Q0, Q1, Q2. Цикл повторения чисел определяется 2m - тактами синхросигнала (максимальный цикл). В таблице состояний генератора чисел использованы (рис. 3.31, а) следующие обозначения: Nп - десятичный эквивалент двоичного числа, реализуемого в параллельном коде; D - функция аргументов Q0, Q1, Q2.

Эту функцию можно рассматривать как последовательный код. Для получения минимальной дизъюнктивной формы записи функции D построим карту Карно (рис. 3.31, б).

Рис. 3.30. Структурная схема трехразрядного генератора чисел на D - триггерах

Схема комбинационного устройства содержит три элемента конъюнкции и один элемент дизъюнкции (рис. 3.32). При построении схемы КУ дополнительные инверторы не потребуются, т.к. триггеры регистра имеют как прямые, так и инверсные выходы.

Использование регистров сдвига в кольцевых схемах представляет практический интерес, так как его структурные схемы состоят из повторяющихся триггерных цепей, обладают наращиваемостью и пригодны для различных применений.

В приложениях приведены схемные обозначения и нумерация выводов регистров, выпускаемых в интегральном исполнении.

RS - триггер: а) - упрощенная таблица состояний; б) полная таблица

переходов; в) Карта Карно; г) RS - триггер, управляемый сигналом низкого

уровня (

триггер); д) RS - триггер на элементах базиса ИЛИ-НЕ

Рассмотрим строку 4. После того, как подается сигнал на вход R, триггер сбрасывается, т.е. переходит из состояния “1” в состояние “0”.

Рассмотрим строку 5. Триггер устанавливается, т.е. переходит из состояния “0” в состояние “1”, в результате подачи сигнала “1” на вход S. Для строк 1 и 2 сигналы S =01* и R=0, и, следовательно, никаких изменений в состоянии триггера не происходит. Для строки 3 сигнал R=1, и этот сигнал в нормальных условиях должен сбросить триггер, но так как триггер уже “сброшен” и Q = 0, то сигнал R = 1 не изменяет его состояние.

Аналогично для строки 6 сигнал S = 1, и этот сигнал в обычных условиях будет устанавливать триггер в “1”, но Q = 1, и, следовательно, состояние триггера останется без изменений до поступления следующего сигнала R.

Особенность RS-триггера заключается в том, что при подаче одновременно на входы R и S сигнала, соответствующего логической 1, состояние триггера становится неопределенным: на обоих выходах Q и `Q установится уровень “1”, а после снятия со входов управляющих сигналов, в силу случайных причин, триггер может установиться в состояние “0” либо “1”. Очевидно, что для нормальной работы триггера необходимо исключить указанное сочетание входных сигналов, приводящее к неопределенному состоянию, что можно осуществить, предусмотрев выполнения запрещающего условия R × S=0.

Из таблицы состояний может быть получено уравнение, описывающее поведение триггера. Это уравнение носит название характеристического уравнения триггера. Оно показывает, как меняется состояние триггера в зависимости от текущих значений состояния и входов.

Для получения упрощенного аналитического выражения, описывающего поведение RS-триггера, построим карту Карно и проведем соответствующие контуры (рис. 3.3, в). Полученное характеристическое уравнение триггера имеет вид

Применив закон де Моргана преобразуем полученные выражение в базис И-НЕ:

Схема RS- триггера, реализованного в выбранном базисе, приведена на рис. 3.3, г.

Из формулы RS - триггера видно, что при реализации его в базисе И-НЕ, триггер управляется сигналами низкого уровня, т.е. уровня лог. "0" (если не предусмотрены инверторы). Для приведения поведения триггера, выполненного на элементах И-HE, в соответствие с таблицей состояний сигналы S и R необходимо инвертировать.

Из анализа схемы рис. 3.3, г очевидно, что простой RS триггер можно сконструировать, соединив “крест-накрест” два элемента И-НЕ.

Входные линии триггера обозначены как

, поскольку триггер устанавливается при

=0 и сбрасывается при

=0. Такой триггер иногда называют RS-триггер с инверсными входами или конъюнктивной бистабильной ячейкой.

Схема RS-триггера, реализовнная в базисе И-HЕ в соответствии с таблицей состояний, приведена на рис. 3.3, д. Для построения RS -триггера на элементах ИЛИ-НЕ приведем формулу триггера в базис ИЛИ-НЕ

Схема RS -триггера, выполненная на элементах базиса ИЛИ-HЕ, приведена на рис. 3.4, а. Временные диаграммы, поясняющие работу RS-триггера, приведены на рис. 3.4, б.

Из временных диаграмм (рис. 3.4, б) следует, что рассмотренные выше RS-триггеры опрокидываются, т.е. управляются сигналами R и S, в любой момент времени. В тех случаях, когда длительности управляющих сигналов не синхронизированы (не согласованы), триггер может находиться в неопределенном состоянии (интервалы времени t4, t5), и поэтому такие триггеры называют асинхронными.

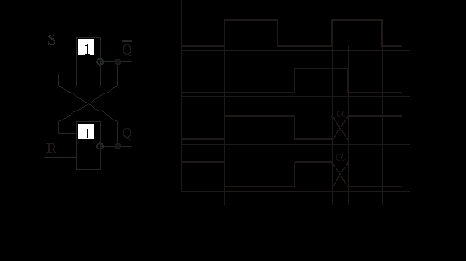
Триггер, построенный на базе элементов ИЛИ-НЕ, называют также дизьюнктивной бистабильной ячейкой. Бистабильные ячейки, помимо самостоятельного применения, входят в качестве составного узла в триггеры других типов.

Синхронный RS -триггер. Синхронные триггеры снабжаются дополнительным входом, по которому поступает синхронизирующий (тактирующий) сигнал. При этом изменение состояния триггера происходит (при наличии управляющего сигнала) только в те моменты времени, когда на специальный синхровход триггера поступает тактирующий импульс (рис 3.5, а). Синхронный RS-триггер строится в соответствии с рис. 3.5, б, а его условное изображение на принципиальных и функциональных схемах приведено на рис. 3.5, в. Синхронизирующий вход обозначается буквой С.

Входные сигналы S и R являются информационными, а на входе С - синхронизирующими, по ним происходит переключение триггера. Следует отметить, что для надежной работы триггера необходимо, чтобы длительность переключающего сигнала (синхронизирующего сигнала) на входе С была не меньше времени переключения триггера. Временем переключения (срабатывания, установки) триггера называется время, которое проходит от момента изменения входных сигналов до соответствующего изменения состояния выходов и определяющееся задержками распространения сигнала логическими элементами, входящими в состав триггера.

Двухступенчатый RS - триггер. Рассмотренные схемы RS-триггеров являются одноступенчатыми. Применение одноступенчатых RS-триггеров в качестве самостоятельных запоминающих элементов ограничено. Это связано с неустойчивой работой последовательностной схемы (цифрового автомата), память которой выполнена на одноступенчатых RS-триггерах. Сигналы переключения триггера S(t), R(t) формируются в цифровом автомате комбинационной схемой, в их формировании участвуют, наряду с внешними логическими сигналами, сигналы Q(t) и

(t). Переключение одноступенчатого триггера под действием сигналов S(t) и R(t) вызывает изменение значений сигналов Q(t) и

(t), а их изменение может привести к изменениям сигналов S(t) или R(t) в том же такте времени t и, как следствие, к ложному срабатыванию триггера. Для устойчивой работы триггера необходимо, чтобы сигналы Q(t) и

(t) изменялись только после прекращения действия входного сигнала S(t) или R(t). Это требование выполняется в двухступенчатых триггерах (MS-триггерах). Базовыми схемами для построения двухступенчатых триггеров являются одноступенчатые RS-триггеры.

Двухступенчатый триггер состоит из двух секций (ступеней), соединенных каскадно, как показано на рис. 3.6 а, причем, каждая секция содержит по синхронному RS-триггеру. Первая секция, ведущая или М-секция (М происходит от английского MASTER) принимает информацию со входных линий S и R. Состояние выходов ведущей секции подается на вторую секцию, ведомую, или S-секцию (S происходит от английского SLAVE).

Для ведущего триггера используется обычная синхронизация, в то время как для ведомого триггера импульс синхронизации инвертируется. Изменение состояния выхода ведущего триггера будет происходить в момент появления положительного импульса синхронизации, и эти изменения будут переданы на входы ведомого триггера. Однако, никакие изменения на выходе ведомого триггера не будут происходить до тех пор, пока не появится положительный сигнал инвертированного импульса синхронизации, т.е. отрицательный (задний фронт) фронт исходного синхроимпульса. Следовательно, изменения на выходах Q и

не произойдет до тех пор, пока не завершится импульс синхронизации. На рис. 3.6, б показаны временные диаграммы работы триггера.

На функциональных схемах двухступенчатый триггер изображается в соответствии с рис. 3.6, в. Символ ТТ в поле условного обозначения означает , что триггер двухступенчатый.

Триггеры с динамическим управлением.

Динамические триггеры могут опрокидываться как передним, так и задним фронтом тактирующих импульсов. Фрагменты схемного обозначения приведены на рис. 3.7.

RS - триггер

3.2. RS - триггер

Важным методом, используемым для описания функционирования RS- триггера, является метод таблиц состояний (таблиц переходов). Таблица состояний (рис. 3.3.а) RS-триггера в сокращенной форме (эту таблицу называют также управляющей таблицей, таблицей функционирования) содержит два входных сигнала (сигналы R и S) и один выходной сигнал Q (функция). Хотя триггеры имеют два выхода - один прямой Q, а другой - инверсный `Q, в описании триггера и в таблице состояний указывают лишь состояние прямого выхода Q.

Из таблицы состояний триггера видно, что при подаче на вход R уровня лог. «1» триггер принимает состояние логического «0», а при подаче управляющего сигнала «1» на вход S - состояние «1». Следует отметить также, что если до подачи управляющего сигнала, например, на вход R, триггер находился в состоянии логического «0», его состояние не изменится и после подачи сигнала «1» на вход R. Если на обоих входах триггера имеются уровни логического «0»- это состояние соответствует режиму хранения и триггер сохраняет предыдущее состояние. В таблице это состояние обозначено условно Q0. При подаче на входы R и S одновременно уровня «1» триггер будет находиться в неопределенном (или неправильном) состоянии, поэтому такое сочетание сигналов R и S называется запрещенной комбинацией управляющих сигналов и в таблице состояний обозначается буквой a.

Сокращенная таблица состояний триггера отражает лишь динамику изменения состояния триггера и не учитывает свойство триггера запоминать единицу информации. Полная таблица состояний триггера должна учитывать влияние (на процесс управления) значения предыдущего состояния триггера Q0. Причем Q0 представляется как входная переменная. Полная таблица состояний RS -триггера приведена на рис. 3.3, б.

Таблицу состояний строят так же, как и таблицу истинности.

Анализ таблицы показывает, что только в ситуациях, описываемых строками 4 и 5, происходит изменение состояния триггера.

Т-триггер

3.5. Т-триггер

Т-триггер - это счетный триггер. Т-триггер имеет один вход (вспомогательные входы принудительной установки “0” и “1” не рассматриваются), куда подают тактирующие (счетные ) импульсы. После подачи каждого тактирующего импульса состояние Т-триггера меняется в обратное (инверсное) предыдущему состоянию (аналогично состоянию JK-триггера при комбинации входных переменных J=1 и K=1). Т-триггеры строятся только на базе двухступенчатых (RS, D, JK) триггеров.

Т-триггер можно синтезировать из любого типа двухступенчатого триггера. Рассмотрим пример синтеза Т-триггера из JK-триггера. Для этого Т-триггер представим как совокупность комбинационного устройства КУ и JK-триггера (рис. 3.19).

Приведенное на рис.3.19, (а) комбинационное устройство должно обеспечить на выходах J и K соответствующие сигналы управления RS-триггером (при подаче на его входы сигналов Q и Т), в соответ-ствии с таблицей состояний (рис. 3.19, б). Карты Карно, с помощью которых получены минимальные формы логических выражений для функций J и K, приведены на рис 3.20.

Из полученных логических выражений следует, что для построения Т-триггера, достаточно объединить входы C, J, K JK-триггера, как показано на рис. 3.21.

Рис. 3.21. Схема Т – триггера, выполненного на базе JK - триггера

Счетный триггер можно синтезировать и на базе D-тригера. Рассмотрим пример реализации Т-триггера на базе D-триггера, управляемого фронтом синхроимпульса. Совмещенная таблица состояний синтезируемого триггера и D-триггера приведена на рис. 3.22, (а). Карта Карно, используемая для минимизации логического выражения функции, КУ, содержит всего один контур с двумя клетками и, следовательно, функция будет содержать тоже всего одну переменную (рис. 3.22, б).

Из логического выражения функции D следует, что для получения счетного триггера из D-триггера, достаточно соединить инверсный выход D-триггера с его входом “D” (рис. 3.23).

Временные диаграммы, поясняющие принцип работы счетного триггера приведены на рис. 3.24. Из временных диаграмм следует, что переключение состояния счетного триггера, выполненного на базе D-триггера, происходит в моменты поступления передних фронтов синхроимпульсов. Частота следования импульсов на выходе счетного триггера в два раза меньше частоты входных синхроимпульсов, что позволяет их использовать в качестве делителей частоты. Если один счетный триггер позволяет делить частоту на два, то для реализации делителя частоты на четыре потребуется два триггера, соединенных последовательно и т.д.

управляемого активным низким уровнем. Сравните

3.1. Опишите работу RS - триггера, управляемого активным низким уровнем. Сравните временные диаграммы работы асинхронного и синхронного RS - триггеров.
3.2. Почему JK- триггер можно построить только на базе двухступенчатых RS либо D - триггеров?
3.3. Попробуйте синтезировать JK- триггер из D- и Т - триггеров.
3.4. Постройте временные диаграммы четырёхразрядного регис-тра сдвига, работающего в режиме деления чисел (в двоичном коде) и объясните принцип его работы.
3.5. Синтезируйте счетчики обратного счета с Ксч =7 на D - и JK - триггерах.
3.6. Нарисуйте схему делителя частоты с Кдел = 171. В схеме можно использовать ИМС КР1554ИЕ23 (см. приложение, стр. 132) и элементы логики этой же серии.

Формирователи импульсов

4.1. Формирователи импульсов

Формирователь коротких импульсов с применением линий задержки. Формирователь коротких импульсов формирует импульсы, длительность которых существенно меньше длительности исходных импульсов. Для построения схемы формирователя потребуются один элемент конъюнкции, один инвертор и линия задержки. Длительность выходного импульса формирователя определяется длительностью времени задержки линии задержки Dtз и средним временем распространения сигнала через инвертор tз срЭ1. На рис. 4.1. приведена схема формирователя, а на рис.4.2 (а) и (б) - временные диаграммы, иллюстрирующие её работу. Из рис 4.2 (а) следует, что для формирования импульса от переднего фронта (исходного импульса) необходимо подавать на линию задержки инвертированный импульс.

В случае формирования импульса от заднего фронта нужно инвертировать незадержанный (прямой) сигнал, т.е. сигнал, подаваемый на элемент “И” минуя линию задержки (рис. 4.2, б).

Использование в формирователях линий задержки не всегда оправдано экономически и из конструктивных соображений. Если не требуется формирование строго определенной длительности коротких импульсов, в формирователях в качестве линии задержки применяются логические элементы (рис. 4.3). Так как каждый логический элемент обладает свойством задерживать распространение сигнала, поэтому время задержки в такой схеме будет определяться числом используемых элементов логики n

Dtз = tз срЭ1 + tз срЭ2 + . . . .+ tз срЭn = n tз срЭ,

где tз срЭ - среднее время задержки одного логического элемента. Считается, что инвертор имеет значительно меньшее время задержки сигнала, и в качестве элементов задержки используются логические элементы с малым быстродействием.

Формирователь импульсов на элементах логики с использованием RC цепи. RC цепи широко применяются в импульсной технике для формирования сигналов различной формы. RC -цепь - это цепь состоящая из сопротивления R и конденсатора С. Постоянная времени этой цепи определяется как t = RC. В зависимости от сочетания соединений RС цепь может выполнять функцию как укорачивающей, так и удлиняющей цепей. Формирователь импульса с удлиняющей RC цепью и его временные диаграммы приведены на рис. 4.4, а и б, соответственно.

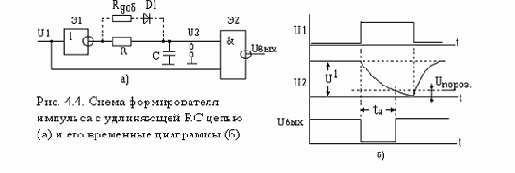Длительность выработанного формирователем импульса можно вычислить исходя из условия разряда конденсатора С. Действительно, пока конденсатор С разряжается до уровня порогового напряжения Uпор, напряжение U2 воспринимается элементом Э2 как уровень логической “1” и на его выходе поддерживается “0”. С течением времени tи напряжение на конденсаторе С становится равным Uпор и на выходе элемента Э2 появится “1”. Если считать, что напряжение до начала разряда на конденсаторе было равно напряжению уровня “1”, т.е. U1, то изменение напряжения Uс с течением времени можно представить как

отсюда имеем

Длительность импульса равна времени разряда конденсатора до порогового значения Uпор

Для ускоренного восстановления заряда конденсатора в схему может быть включен дополнительный диод D1 (рис. 4.4, а). Из-за большого обратного сопротивления диода его влияние в процесс разряда конденсатора можно не учитывать, т.е. разряд конденсатора будет осуществляться только через сопротивление R.

В тех случаях, когда требуется получить импульсы большой длительности и в схеме используется конденсатор большой емкости, последовательно с диодом включают дополнительное сопротивлени Rдоб, ограничивающее ток заряда конденсатора. Величину сопротивления R выбирают исходя из следующих условий:

во-первых, величина сопротивления R не должна превышать максимально допустимого значения, при котором на этом сопротивлении за счет обратного входного тока элемента логики может создаться напряжение, сравнимое с напряжением Uпор (для элементов ТТЛ структуры максимальное значение Rмак = 2,2 кОм);

во-вторых, минимальное значение сопротивления ограничено допустимой нагрузочной способностью логического элемента Э1 и определяется как

где U1 - напряжение на выходе элемента Э1 в состоянии логической “1”; n - коэффициент разветвления (нагрузочная способность) выхода логического элемента; Iвх - входной ток одного элемента.

Номинал добавочного сопротивления имеет ограничение “снизу”, и определяется из условия

где Uпр D1 - прямое падение напряжения на диоде D1; I1доп - допустимый выходной ток элемента Э1 в состоянии логической “1”.

Схема формирователя коротких импульсов с помощью укорачивающей (дифференцирующей) RC цепи показана на рис. 4.5. Длительность выходного импульса формирователя может быть определена из соотношения

где Rвых - выходное сопротивление первого элемента формирователя.

Триггер Шмитта. Триггер Шмитта применяется для формирования входного сигнала произвольной формы в сигналы, принимающие два стандартных уровня ”0” и “1”. Варианты схем таких формирователей показаны на рис. 4.6.

На рис. 4.6, а показана схема триггера Шмитта, в которой применены два инвертора, входящие в серию логических транзисторно-транзисторных интегральных схем. Положительная обратная связь между инверторами обеспечивается за счет резистора R1, включенного в общую цепь питания элементов. Для увеличения влияния цепи обратной связи, ток через второй инвертор увеличен путем включения дополнительного резистора R2 между выходом Э2 и источником питания. Подобный формирователь на интегральных схемах серии К1533 удовлетворительно работает до частоты несколько мегагерц при подаче на вход синусоидального напряжения амплитудой 0,5 - 0,8 В.

В триггерах Шмитта положительную обратную связь можно ввести также путем включения резистора между выходом второго инвертора и входом первого (рис. 4.6, б). Входное напряжение в этом формирователе подается через дополнительный резистор R1, сопротивление которого также влияет на глубину положительной обратной связи. Увеличение сопротивления этого резистора увеличивает коэффициент положительной обратной связи и уменьшает чувствительность формирователя к входному напряжению.

На практике, в качестве формирователей импульсов, часто применяют специальные интегральные схемы формирователей (рис. 4.6, в). Обозначение функционального назначения таких интегральных схем содержит две буквы “ТЛ”. Например, в серии К155: это интегральные микросхемы (ИМС) К155ТЛ1, К155ТЛ2, К155ТЛ3.

Формирователь импульсов от механических контактов. При проектировании цифровых устройств часто возникает задача четкого формирования импульсов от механических контактов (при срабатывании реле, кнопок, переключателей и т.д.), так как непосредственная подача этих сигналов на входы цифровых устройств недопустима из-за “дребезга” контактов. Дребезг контактов - это явление многократного неконтролируемого замыкания и размыкания контактов в моменты их соприкосновения и расхождения. Это явление приводит к формированию пачки импульсов (вместо требуемого одиночного импульса или перепада напряжения), могущих вызвать многократное непредсказуемое срабатывание триггеров и счетчиков схемы цифрового устройства.

Существует множество вариантов построения цепей подавления импульсов дребезга контактов с помощью статического триггера, дифференцирующей и интегрирующей цепей, а также узла, обладающего свойствами интегрирующей цепи и триггера Шмитта. На рис. 4.7 приведены примеры схем подавления “дребезга” контактов.

Наиболее надежной и простой в схемном решении является схема подавления дребезга на статическом RC - триггере (рис. 4.7, а). Сигнал “0”, подаваемый с помощью переключателя к одному из входов этого триггера опрокидывает его. Причем при каждом срабатывании переключателя (кнопки) триггер реагирует на первое же замыкание соответствующей контактной пары и последующие замыкания уже не изменяют его состояние.

Недостатком такой схемы подавления дребезга является необходимость использования контактов на переключение, что не всегда приемлемо. В тех случаях, когда кнопка (переключатель) имеет всего одну пару контактов только на замыкание, применяются схемы, использующие постоянную времени перезаряда конденсатора.

Формирователь, показанный на рис. 4.7, б лишен этого недостатка. Он состоит из триггера Шмитта, на входе которого включена интегрирующая цепь (R2, C). При замыкании контактов кнопки SB напряжение на входе цепи R2 C падает до нуля. Возникающее в процессе переключения кратковременные импульсы, вызванные “дребезгом”, сглаживаются интегрирующей цепью. Постоянная времени интегрирующей цепи выбирается так, чтобы амплитуда пульсаций сигнала на её выходе была меньше порога чувствительности триггера Шмитта.

Рассматриваемый формирователь может работать и без сопротивления R2 (его включают в качестве токоограничивающего сопротивления через замкнутые контакты кнопки). Благодаря малому сопротивлению замкнутых механических контактов первое же их замыкание приводит к полному разряду конденсатора. Последующие же размыкания контактов, вызванные дребезгом, практически не увеличивают напряжение на конденсаторе вследствие относительно большой постоянной времени его заряда.

Формирователь импульсов на одном инверторе (рис. 4. 7, в) позволяет получить относительно большую постоянную времени перезаряда конденсатора при малой его емкости. При замыкании контактов кнопки конденсатор С быстро разряжается через R2. В отличие от рассмотренных выше формирователей, здесь на выходе вырабатывается импульс, длительность которого определяется постоянной времени RC цепи.

Для формирования импульсов от механических контактов можно использовать также одновибратор, схема которого будет рассмотрена ниже.

Генераторы импульсов

4.2. Генераторы импульсов

Генератор одиночных импульсов (ждущий мультивибратор). Ждущий мультивибратор называют также одновибратором. Одновибраторы предназначены для вырабатывания одиночных импульсов с заданной длительностью. При этом длительность запускающего импульса особой роли не играет, лишь бы она была не больше длительности вырабатываемого одновибратором импульса, т.е. tи зап<tи, где tи зап - длительность запускающего импульса; tи - длительность выходного импульса одновибратора.

Схема одновибратора приведена на рис. 4.8, а. Он выполнен на двух элементах логики типа 2И-НЕ путем введения положительной обратной связи (выход второго элемента соединен с входом первого).

В исходном состоянии на выходе элемента Э2 имеется уровень “1”, а на выходе элемента Э1- “0”, так как на обоих его входах имеется “1”(запускающие импульсы представляют отрицательный перепад напряжения). При поступлении на вход запускающего отрицательного перепада напряжения на выходе первого элемента появится уровень “1”, т.е. положительный скачок, который через конденсатор С поступит на вход второго элемента. Элемент Э2 инвертирует этот сигнал и уровень “0” по цепи обратной связи подается на второй вход элемента Э1. На выходе элемента Э2 поддерживается уровень “0” до тех пор, пока не зарядится конденсатор С до уровня Uc пор = U1 - Uпор, а напряжение на резисторе R не достигнет порогового уровня Uпор (рис. 4.8, б).

Длительность выходного импульса одновибратора может быть определена с помощью выражения

где Rвых - выходное сопротивление первого элемента. Uпор - пороговое напряжение логического элемента.

Несимметричный мультивибратор. На базе логических элементов можно построить различные генераторы импульсов. Наиболее широкое применение в цифровых устройствах нашли два типа - несимметричный и симметричный мультивибраторы. В несимметричном мультивибраторе (рис. 4.9, а) резистор R выводит в усилительный режим первый инвертор, а выходное напряжение этого инвертора должно удерживать в режиме усиления второй инвертор. Положительная обратная связь через конденсатор С вызовет мягкое (не нуждающееся в первоначальном толчке) самовозбуждение автоколебательного релаксационного процесса. Период Т импульсов, вырабатываемых мультивибратором, определяется в первом приближении постоянной времени t = RC (Т = а t, где а обычно имеет значение 1...2). Частоту следования импульсов можно оценить (с точностью до 10 %) из выражения f = 1/2RC.

Симметричный мультивибратор. Схема симметричного мультивибратора показана на рис. 4.9, б. Симметричность выходных импульсов может быть достигнута при выполнении условий: R1 = R2; C1 = C2. Период следования импульсов Т определяется как сумма двух времен заряда конденсаторов, т.е.

Т = tзар1 + tзар2 ,

где tзар1 = t1 ln(U1/Uпор); tзар2 = t2 ln(U1/Uпор).

Значения t1 и t2 определяются с учетом выходных сопротивлений инверторов Rвых Э1 , Rвых Э2

t1 = С1 (R2 + Rвых Э1)

t2 = С2 (R1 + Rвых Э2).

Частота следования выходных импульсов симметричного мультивибратора определяется из соотношения:

Генераторы линейно изменяющего напряжения (ГЛИН). ГЛИН представляют собой электронные устройства, выходное напряжение которых в течение некоторого времени изменяется по линейному закону. Часто такое напряжение меняется периодически. В этом случае ГЛИН называется генератором пилообразного напряжения (ГПН) или генератором напряжения треугольной формы (рис. 4.10, а, б). Если напряжение меняется от минимального значения к максимальному (по абсолютной величине), то его называют линейно-нарастающим напряжением. Если меняется от максимального значения к минимальному - линейно-падающим.

ГЛИН нашли широкое применение в отклоняющих системах осциллографов, телевизоров, в радиолокации, в преобразователях “напряжение-временной интервал”, широтно-импульсных модуляторах и т.д.

ГЛИН строятся на принципе заряда и разряда конденсатора. Схема простейшего ГПН, работающего по принципу заряда конденсатора, показана на рис. 4.10, в. Она состоит из времязадающего конденсатора С, резистора Rк и транзисторного ключа VT1. На вход транзисторного ключа подается последовательность прямоугольных импульсов с заданным интервалом между импульсами и длительностью (рис. 4.10, г). Когда на базе транзистора нулевое напряжение (промежуток времени между импульсами), транзистор закрыт и происходит заряд конденсатора через резистор Rк. Если постоянная времени цепи Rк C достаточно большая, т.е. существенно больше периода следования прямоугольных импульсов, напряжение на конденсаторе нарастает линейно. Заряд конденсатора продолжается до поступления импульса, открывающего транзистор VT. Когда транзистор открывается, начинается процесс разряда конденсатора. Интервал времени между отпирающими импульсами должен быть достаточным для полного разряда конденсатора С.

Напряжение на конденсаторе изменяется по закону:

где t = RC - постоянная времени цепи, состоящей из Rк и С; t - текущее значение времени, когда t=0, Uс = Еп(1- 1) = 0.

Известно, что функцию ех можно представить в виде степенного ряда

Для значений Х<<1 функцию можно определить первыми двумя членами ряда

ех = 1+Х,

тогда, используя это выражение для случая заряда конденсатора при t<<t, определяем напряжение на конденсаторе

Uc = Eп(1-

где t/t <<1.

Очевидно, что в случае использования этого процесса в ГПН, t = tи = tзар; t = Rк С, тогда

Линейно изменяющееся напряжение Uc (t) характеризуется рядом параметров:

- длительностью прямого хода tпр, т.е. временем, в течение которого конденсатор заряжается через сопротивление Rк до напряжения Uc;

- длительностью обратного хода to (время восстановления) - это время, в течение которого происходит разряд конденсатора;

- периодом повторения линейно изменяющегося напряжения (пи-лообразных импульсов) T = to + tпр;

- амплитудой пилообразных импульсов Um;

- коэффициентом нелинейности g.

Одним из самых важных параметров ГЛИН является коэффициент нелинейности. Для определения g воспользуемся известным утверждением, что линейная функция характеризуется постоянством производной во всех её точках, поэтому отклонение от линейного закона можно оценить коэффициентом нелинейности. Нелинейность определяется максимальным отклонением реальной формы сигнала от идеальной линейной формы. Коэффициент нелинейности находят как отношение изменений производных функции в начале и в конце процесса нарастания

Учитывая, что dUc/dt = ic/C, где ic - ток заряда конденсатора, можно получить удобное для расчетов выражение

где iн - ток заряда конденсатора в начале процесса (импульса); iк - ток заряда к моменту окончания импульса.

Если пренебречь обратным током транзистора и током утечки конденсатора iн можно определить как

iн = Еп / Rк.

В конце импульса напряжение, заряжающее конденсатор С, будет меньше напряжения источника питания на величину Um, следовательно, ток в конце будет определяться как

iк = (Еп - Um) / Rк.

Так как при tпр <<t Um = Uc = Eп tпр/ RC, окончательное выражение коэффициента нелинейности будет иметь вид

Простейший генератор линейного напряжения характеризуется также коэффициентом использования напряжения источника питания

x = Um / Eп.

Если подставить значение Um в выражение для коэффициента использования напряжения источника питания, получим

x =

Из полученного выражения для коэффициента нелинейности следует, что чем лучше линейность пилообразного напряжения, тем меньше амплитуда напряжения ГЛИН. Например, если напряжение источника питания 10 В, для получения коэффициента нелинейности g = 1 % амплитуда напряжения импульсов ГПН не должна превышать 0,1 В.

Для повышения коэффициента использования напряжения питания при малых значениях коэффициента нелинейности применяются стабилизаторы постоянного тока (ГСТ). Действительно, из выражения для g видно, что при обеспечении постоянства тока заряда (для линейно падающего напряжения - тока разряда) iн = iк, следовательно g®0.

Схема простого генератора пилообразного напряжения со стабилизатором тока в цепи разряда конденсатора показана на рис. 4.11, а. Заряд конденсатора осуществляется через транзистор VT1 и сопротивление Rк. За время заряда напряжение на конденсаторе достигает практически напряжения источника питания. Когда приходит на базу транзисторов нулевой уровень, первый транзистор закрывается, а транзистор VT2 переходит в режим генератора стабильного тока (ГСТ) и через него протекает стабильный постоянный ток разряда конденсатора (рис. 4.11, б).

При определении коэффициента нелинейности импульсов этого генератора пилообразного напряжения необходимо учитывать влияние сопротивления нагрузки Rн на процесс разряда конденсатора. Ток через сопротивление нагрузки обусловлен напряжением на конденсаторе и в конце разряда он равен нулю, так как к концу разряда Uc = 0. С учетом высказанных соображений можно получить выражение для коэффициента нелинейности ГПН с генератором стабильного тока.

Из полученного выражения следует, что для уменьшения g желательно использовать высокоомные нагрузки или же уменьшать амплитуду импульса сигнала.

Применение элементов логики в модуляторах звуковых

4.3. Применение элементов логики в модуляторах звуковых

сигналов

Модулятор с подавлением постоянной составляющей сигнала. Принципиальная схема модулятора, предназначенного для преобразования аналогового сигнала в последовательность импульсов постоянной амплитуды и с переменной длительностью, представлена на рис. 4.12.

Закон изменения длительности импульсов определяется законом изменения входного сигнала, подаваемого на затвор полевого транзистора через конденсатор С2. На элементах D1.1 и D1.2 выполнен генератор прямоугольных импульсов со скважностью 2. Частота следования импульсов генератора около 50 кГц. Сопротивление R1 и диод VD1 служат для получения “меандра”, то есть для выравнивания времен заряда и разряда конденсатора С1.

Импульсная последовательность с выхода генератора (элементы D1.1, D1.2) в прямом виде поступает на запускающий вход модулирующего одновибратора, выполненного на элементах D2.1, D2.3, а в инверсном виде - на вход схемы приращения на элементе D2.2. Изменение длительности импульсов, то есть модуляция входного сигнала, осуществляется за счет динамического сопротивления канала исток-сток полевого транзистора VT1. Сопротивление канала исток-сток данного транзистора зависит от напряжения смещения, подаваемого на его затвор. Причем, при прямом смещении на затворе (относительно стока на затворе и на истоке положительные потенциалы) сопротивление канала может изменяться в пределах 0.5- 300 кОм в диапазоне напряжений смещения от нуля до трех вольт. Транзисторы КП103Ж имеют крутизну изменения сопротивления около 1 кОм/мВ при начальном смещении 1.8 -2.2 В. При приращениях напряжения 0.15...0.2 В крутизна изменения сопротивления Sr практически линейна.

Известно, что длительность импульса, вырабатываемого одновибратором определяется как

tи = RC ln (U1/Uпор), (4.1)

где R- действующее сопротивление участка исток-сток транзистора VT1 с учетом сопротивления R3 (рис. 4.12 ); С- емкость конденсатора С2; U1- напряжение на выходе элемента в состоянии логической единицы и Uпор- пороговое напряжение, по достижении которого на входе, логический элемент переходит в инверсное, относительно исходного, состояние. С учетом крутизны изменения сопротивления Sr длительность импульса tи(uc) можно представить в виде

tи(uc) = (Uсм + Uc) Sr C ln(U1/Uпор)=

=SrC (Uсм + Um SinWt) ln(U1/Uпор), (4.2)

где Um - амплитуда входного гармонического сигнала; W - частота модулирующего сигнала; Uсм - напряжение смещения.

Сопротивление R3 служит для выравнивания крутизны Sr при больших значения сопротивления канала транзистора, а также с его помощью можно в значительных пределах изменить чувствительность модулятора. При использовании полевых транзисторов типа КП103 с соответствующими буквенными обозначениями, экспериментально полученная максимальная чувствительность 140 мВ, минимальная чувствительность - 320 мВ.

С целью значительного уменьшения тока потребления каскадами усиления мощности в режиме покоя (то есть когда входной сигнал отсутствует), в модуляторе реализован принцип подавления постоянной составляющей модулированного сигнала, для чего формирование модулированных импульсов от положительной и отрицательной полярности модулирующего сигнала осуществляется по двум каналам. Выходные сигналы положительной полярности формируются последовательностью Q1, отрицательные Q2. Сигнал Q2 (инвертированный Q1) служит для улучшения эксплуатационных свойств модулятора и для автоматической установки длительности импульсов в режиме покоя. Подавление постоянной составляющей осуществляется за счет выделения из модулированных по длительности импульсов приращений, свойственных только выбранному каналу.

Временные диаграммы, иллюстрирующие принцип работы модулятора с подавлением постоянной составляющей, представлены на рис. 4.13.

Из временных диаграмм очевидно, что для полного подавления постоянной составляющей требуется практически полное соответствие последовательностей импульсов на входе и на выходе модулирующего одновибратора. Однако, если учесть (4.1), определяющую длительность импульсов на выходе одновибратора, фронты импульсов, выше упомянутых импульсных последовательностей, когерентны только в "точках" запуска, а внутри цикла генерации могут иметь произвольную временную ориентацию. Причем, нарушение когерентности фронтов импульсов (в отсутствии модулирующего сигнала) вызовет появление сигналов отклика на выходе соответствующего канала. Так, например, смещение фронта импульса вправо (т.е. импульс стал короче) приводит к появлению отрицательных перепадов в канале Q1, что в свою очередь приводит к частичному разряду конденсатора С3 через резистор R6 и диод VD3, и снижению напряжения смещения на затворе транзистора VT1. Уменьшение напряжения смещения приводит к уменьшению сопротивления канала транзистора и частичному увеличению длительности импульса и т.д.

Постоянная времени t =С3R5 =С3R6 выбирается по критериям определения постоянной времени схем автоматической регулировки усиления (АРУ).

Экспериментальные исследования показывают, что t должно быть более 100 мсек. В случае использования источника сигнала с малым входным импедансом необходимо учитывать влияние цепи R4C2Р, выполняющей роль цепи развязки, где сопротивление R4 определяет значение входного сопротивления модулятора. При использовании в схеме модулятора интегральных схем КМОП структуры, потребляемая им мощность не превышает 0.2 мВт. Уровни выходных сигналов определяются значением напряжения питания, при этом амплитуда выходного напряжения не достигает значения напряжения питания, если нагрузка имеет чисто активный характер.

Выходная цепь (рис.4.14) подключается к точкам Q1 и Q2 модулятора. Для измерения выходного сигнала с помощью измерительных приборов с общим "заземлением" необходимо иметь источник питания модулятора, не имеющего заземления.

При напряжении источника питания Еп= 2.8 В; ток потребляемый от источника питания Iп = 65 мкА; частота следования высокочастотной импульсной последовательности f=50 кГц; индуктивность фильтра НЧ Lф=50 мГн; емкость фильтра Сф= 0.1 мкФ; сопротивление нагрузки Rн=2 кОм.

На рис.4.15 приведены зависимости Uвых=f(Uвх) для двух значений сопротивления R3, ограничивающего предельное сопротивление канала модулирующего транзистора VT1 (см.рис.4.12).

Номиналы резистора R3 могут быть различными в зависимости от используемого в схеме транзистора VT1. Как следует из рис.4.15, увеличение R3 может привести к значительному росту чувствительности модулятора, однако его характеристика при этом имеет нелинейный характер. Чрезмерное увеличение R3 приводит также к перемодуляции, вызывающей большие нелинейные искажения выходного сигнала. Номинальное значение Uвх находится в пределах 100 –150 мВ. Увеличение входного напряжения выше указанных значений не приводит к заметному увеличению Uвых, хотя может наблюдаться рост уровня нелинейных искажений. Следует отметить, что при использовании этого модулятора в аппаратах индивидуального пользования, свойство нелинейной зависимости Uвых=f(Uвх) может оказать положительную услугу, как ограничитель амплитуды при больших входных сигналах.

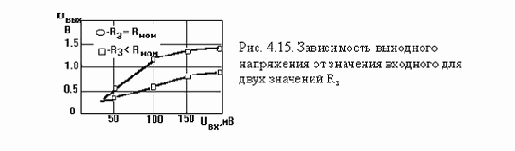Когда отсутствует входной сигнал, на выходе модулятора также должны отсутствовать импульсы генератора, что обеспечивается симметричностью импульсов на выходе элемента D1.3 и генератора (в точке 4, рис. 4.12), то есть параметры емкости С2 и сопротивление участка сток-исток полевого транзистора должны обеспечить такую постоянную времени tm, при которой ждущий мультивибратор, выполненный на элементах D2.1 и D1.3, должен вырабатывать меандр. Поскольку емкость конденсатора С2 не поддается регулировке, подбор tm осуществляется путем изменения смещения на затворе VT1, при котором происходит изменение сопротивления канала сток-исток полевого транзистора. "Жесткая" установка режима работы транзистора снижает температурную и параметрическую стабильность tm (при замене транзистора и т.д.), поэтому, с целью повышения стабильности параметров модулятора, в нем предусмотрена автоматическая установка напряжения смещения на затворе VT1 с помощью цепей обратной связи, состоящих из R5, R6, C3, VD2, VD3 и инвертора D1.6. Принцип работы этой цепи аналогичен принципу работы цепей автоматической регулировки усиления (АРУ), применяемых в радиоэлектронной аппаратуре.

Путем подбора номиналов элементов цепей обратной связи, можно получить оптимальные характеристики модулятора. Отметим, что увеличение постоянной времени (tm =R5C3=R6C3) улучшает линейность модуляционной характеристики модулятора, однако, при этом снижается чувствительность схемы к продуктам несимметричности импульсов модулятора в отсутствии входного сигнала. Зависимости выходного напряжения модулятора для двух значений Uвх при Fн=1 кГц приведены на рис. 4.16. Уменьшение Uвых при малых значениях tm объясняется влиянием отрицательной обратной связи, причем, как и при любой другой отрицательной обратной связи, коэффициент передачи схемы уменьшается.

Как следует из рис. 4.16, с уменьшением уровня входного сигнала зависимость Uвых от постоянной времени цепи обратной связи становится слабее, так как импульсы "ошибки", появляющиеся на выходе модулятора в режиме покоя, становятся соизмеримыми по длительности с импульсами, появляющимися в результате модуляции низкими уровнями входного сигнала.

Наиболее оптимальным при использовании ИМС серии К564, К561 является постоянная времени tm более 50 мс и менее 100 мс. Оптимальное значение постоянной времени, в каждом конкретном случае, определяется индивидуальными особенностями усилителя и его назначением и выбирается при практической реализации модулятора. На рис. 4.17 приведены зависимости Uвых от частоты звукового сигнала Fн при двух значениях tm.

Широтно-частотный импульсный модулятор. Получение наибольшего КПД ключевых усилителей достигается при использовании схемы широтно-частотно-импульсного модулятора. Схема модулятора отличается малым потребляемым током - 35 мкА в режиме покоя и менее 20 мкА - в режиме модуляции (его уникальность заключается и в этом тоже). Этот модулятор можно отнести к классу дельта-модуляторов с переменным шагом квантования. В режиме покоя модулятор вырабатывает импульсную последовательность “меандр” с частотой 50 кГц (при напряжении питания 2.7 В). Симметрия "плеч" импульсов достигается подбором номиналов резисторов R2 и R3. Емкость конденсатора C2 определяет в основном частоту импульсов и на симметрию импульсных перепадов практически не влияет. В качестве элементной базы (D1, рис.4.18) можно использовать ИМС серии К1533, К555, К561, К564 и т.д. Выбор той или иной серии определяет только энергетическая сторона, то есть экономичность схемы модулятора с точки зрения энергопотребления. При использовании микросхем с повышенной частотой переключения с целью стабилизации шага квантования, между выходом Э2 и входом Э1 включают сопротивление положительной обратной связи Rх.

Входное сопротивление модулятора определяется номиналом резистора R1. Это сопротивление определяет также и чувствительность модулятора, причем, чем больше R1, тем меньше чувствительность схемы. Чувствительность модулятора определяется и емкостью конденсатора С2. При уменьшении номинала C2 увеличивается частота импульсов и уменьшается чувствительность модулятора. Критерии чувствительности можно сформулировать двояко, то есть как изменение выходного восстановленного сигнала при определенном изменении входного, например

К= D Uвых / D Uвх ,

или же как

К= DТи / D Uвх ,

где Ти - приращение длительности импульса по абсолютной величине при воздействии входного сигнала с приращением DUвх. Применение дельта-модуляции, при оптимальном подборе параметров схемы, дает возможность увеличения КПД усилителя на 2...5 %. При выборе номиналов элементов схемы исходят из возможности получения оптимальной частоты квантования, позволяющей получить простую схему фильтрации и минимальные нелинейные искажения усиленного сигнала. Известно, что при использовании ШИМ частота следования импульсов в основном определяется из условия оптимальной фильтрации, а в схемах с дельта-модуляцией (частотно-широтно-импульсной модуляцией), адаптивной как по длительности так и по уровню, частота импульсов fи должна удовлетворять условию

где Um вх - максимальное значение амплитуды преобразуемого сигнала; Fв - верхняя частота преобразуемого сигнала; Dкв - шаг квантования, определяемый как абсолютная разрешающая способность модулятора.

Квант напряжения Dкв может быть определен из условия обеспечения необходимого динамического диапазона и допустимого значения амплитуды шумов квантования.

Очевидно, что амплитуда шумов квантования не может быть больше, чем уровень сигналов шумов, имеющихся на входе модулятора.

Если учесть, что амплитуда шумов квантования определяется как

Umш= Dкв / 2, (4.3)

то максимальный квант напряжения должен быть меньше, чем 2Umш с одной стороны, с другой - квант напряжения должен быть меньше чем сигнал шума, вызванный каскадом предварительного усиления (микрофонным усилителем).

Исходя из требований, предъявляемых к усилителям аппаратов индивидуального пользования, напряжение шумов, приведенные к входу усилителя, должно быть не более 3 мкВ, то есть

Uш=Uш вых / К, (4.4)

где К- коэффициент усиления усилителя предварительного каскада; Uш вых - напряжение шумов на выходе этого каскада.

Используя соотношение (4.3) можно получить

Dкв<2КUш = 6К 10-6 В. (4.5)

Из условия обеспечения необходимого динамического диапазона шаг квантования Dкв может быть определен из соотношения

Dкв = Umвх / D, (4.6)

где D=Umвх/Uвх min - динамический диапазон сигнала; Uвх min- минимальное значение амплитуды входного сигнала.

Выражение (4.6) получено из предположения, что шаг квантования не должен быть больше, чем минимальное значение амплитуды входного сигнала. После определения расчетных значений Dкв из соотношений (4.5), (4.6) проверяется соответствие Dкв условию

Dкв > dк + Uсм ,

где dк- погрешность сравнения компаратора; Uсм - напряжение смещения компаратора, приведенное к входу.

Из приведенных выше соотношений следует, что максимальный шаг квантования можно получить при максимальном значении напряжения на входе модулятора. Установленное значение шага квантования имеет силу только для фиксированного значения напряжения питания. С изменением напряжения питания изменяется частота, следовательно и шаг квантования.

Модулятор, схема которого приведена на рис.4.18, совмещает и генератор прямоугольных импульсов, и модулирующий узел. Отсутствие отдельного генератора в модуляторе способствует как упрощению аппаратной части устройства, так и уменьшению энергопотребления схемой.

На рис.4.19 приведена зависимость частоты генерации от значения напряжения питания Еп модулятора, выполненного на базе транзисторов ИМС КМОП структур. Известно, что основной ток потребления микросхем КМОП структуры определяется частотой переключения их элементов и напряжением питания. Увеличение напряжения питания приводит также к росту крутизны сквозных характеристик транзисторов и к уменьшению выходного импеданса микросхем. Последние два фактора являются определяющими в зависимости частоты от напряжения источника питания.

Как следует из рис. 4.19, обе зависимости имеют явно выраженный нелинейный характер. Увеличение частоты генерации с увеличением Uп, объясняется как уменьшением входного импеданса элементов схемы, так и ростом крутизны сквозной характеристики каждого элемента. Исследования показали, что характер зависимости fи от напряжения питания мало зависит от начального значения частоты генерации, устанавливаемого путем подбора номиналов конденсатора С2 и резисторов R2,R3.

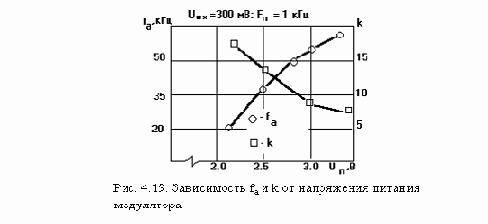Отметим, что при установке начальной частоты генерации предпочтительней является ее установка путем подбора номиналов резисторов R2 и R3, а значение емкости С2 необходимо выбрать как можно меньше. Такой подход позволяет существенно уменьшить ток, потребляемый модулятором. Изменение крутизны модуляционной характеристики k в зависимости от Uп может играть положительную роль при стабилизации уровня выходного сигнала.

Зависимость тока потребления от напряжения питания приведена на рис. 4.20. Из рис. 4.20 следует, что потребляемый модулятором ток зависит также и от частоты следования импульсов. На графиках показаны зависимости для трех частот fи, установленных при напряжении питания Uп = 2.7 В. Веерообразные расхождения кривых зависимости Iпот=f(Uн) при различных значениях начальной частоты объясняется изменением этих частот при изменении напряжения питания Uп (см. рис. 4.19). Как было уже сказано, частоты f1, f2, f3 установлены путем подбора емкости С2 при напряжении питания 2.7 В.

f1=42кГц, f2=50кГц, f3=61кГц.

Практически доказано, что наиболее оптимальной является частота импульсной последовательности равная f2=50 кГц. При построении ключевых усилителей, использующих рассматриваемый тип модулятора, следует применять именно такую частоту (f2=50 кГц).

Следует отметить также, что при применении рассматриваемого модулятора необходимо учитывать его свойство уменьшения тока потребления при увеличении модулирующего напряжения. Это свойство может вызвать особый интерес при построении микромощных усилителей, в частности усилителей "ушных" слуховых аппаратов. На рис. 4.21 представлены зависимости потребляемого модулятором от источника питания тока от амплитуды входного сигнала для трех значений начальной частоты fи. Наблюдаемая стабилизация потребляемого тока при достижении Uвх определенного уровня, по-видимому связана с перехватом "инициативы" генерации в модуляторе сигналом звуковой частоты, а так как все измерения проводились на одной частоте входного сигнала Fн=1 кГц (согласно стандартам измерения параметров усилителей слуховых аппаратов), все три кривые графика (рис. 4.21) сливаются на одном уровне тока потребления, т.к. конечная частота (частота генерации при максимальном входном напряжении) генерации модулятора становится соизмеримой с частотой модулирующего сигнала.

Поведение зависимости Iпот = f(Uвх) особый интерес вызывает при повышенных частотах следования импульсов, когда начальный ток потребления модулятором существенно превышает ток, потребляемый в динамическом режиме. Следует отметить, что подобным свойством обладают лишь схемы частотно-широтно-импульсных модуляторов, реализованных на базе транзисторных структур КМОП ИМС.

Кажущаяся "незначительность" уменьшения Iпот при росте уровня Uвх может оказаться весьма обманчивой при построении усилителей слуховых аппаратов, встраиваемых в ухо человека. Подобные аппараты имеют выходную мощность порядка 0.1...0.2 мВт, соизмеримую с сэкономленной на модуляторе мощностью, а общий, потребляемый усилителем, ток не превышает 1,5 - 2 мА.

Будет ли работать формирователь коротких

4.1. Будет ли работать формирователь коротких импульсов, если число элементов задержки четное? Если да, то как будет выглядеть сформированный импульс?
4.2. Попробуйте перечислить функциональные отличия схемы формирователя импульса с удлиняющей RC цепью от схемы с дифференцирующей цепью.
4.3. Какую роль играет в триггерах Шмитта положительная обратная связь?
4.4. На рисунке 4.7 приведены схемы формирователей импульсов от механических контактов. Какие дополнительные схемы и способы можете предложить для формирования импульсов от механических контактов?
4.5. Почему значение частоты генераторов импульсов, построенных с использованием времязадающих RC цепей определяется только приближенными соотношениями (fи @ 1/ 2RC)?
4.6. Можно ли использовать ГЛИН в качестве автогенератора импульсов?
4.7. Можно ли использовать цифровые элементы логики при обработке аналоговых сигналов?
4.8. Какие типы ИМС целесообразнее применять в различных узлах формирователей импульсов?

Аналого-цифровые преобразователи

5.2. Аналого-цифровые преобразователи

Аналого-цифровые преобразователи (АЦП) предназначены для преобразования аналоговых (непрерывных) сигналов в цифровую форму. Преобразование аналогового сигнала происходит в определенные моменты времени, которые называются точками отсчета. Количество отсчетов за единицу времени определяет частоту дискретизации (преобразования), которая, в свою очередь, определяется быстродействием и условиями использования АЦП. Интервал времени между отсчетами Тотс и частота дискретизации fпр связаны соотношением:

Тотс = 1/fпр.

В измерительной технике для преобразования медленно меняющихся процессов частота преобразования может быть установлена небольшой - единицы Герц и менее. В устройствах, где требуется преобразовывать сигналы в масштабе реального времени, частота преобразования выбирается из условия достижения максимальной точности восстановления цифрового сигнала в аналоговую форму. Например, преобразование речевого сигнала в дискретную форму. При этом частота дискретизации определяется как fпр = 2Fмах, где Fмах - максимальная частота речевого сигнала.

Для обеспечения преобразования без искажений требуется выполнение условия:

tпр < Тотс,

где tпр - время преобразования АЦП одного отсчета.

Основные параметры АЦП определяются также как и параметры ЦАП (см. п. 5.1) .

По принципу дискретизации и структуре построения АЦП делятся на две группы: 1-группа АЦП с применением ЦАП и 2-группа АЦП без ЦАП.

К первой группе относятся:

- АЦП последовательного счета (развёртывающего типа);

- АЦП последовательного приближения (поразрядного уравновешивания);

- следящий АЦП.

К второй группе относятся:

- АЦП прямого преобразования;

- АЦП двойного интегрирования;

- АЦП с применением генератора, управляемого напряжением (ГУН).

Каждый тип АЦП имеет свои достоинства и недостатки. На практике встречаются все выше перечисленные типы АЦП.

Области применения ЦАП и АЦП. С помощью АЦП и ЦАП можно организовать обмен информацией с ЭВМ в масштабе времени сигналов звукового вещания. Структурная схема терминала приведена на рис. 5.9, а. С выхода магнитофона М1 аналоговый сигнал поступает на вход АЦП, где преобразуется в цифровой код, который подается на вход устройства сопряжения УС1. В устройстве сопряжения преобразованные АЦП сигналы синхронизируются и согласовываются с сигналами блока управления БУ1, который дает команду о прохождении информации в память ЭВМ. Вывод обработанного цифровыми методами сигнала звукового вещания из ЭВМ на второй магнитофон М2 осуществляется с помощью ЦАП. Информация считывается из памяти ЭВМ и поступает на вход блока стандартного сопряжения (БСС). После реализации команд управления информация поступает на устройство вывода УС2 и через БУ2 на вход ЦАП.

АЦП и ЦАП широко применяются и в речевых терминалах (рис. 5.9 ,б). В таких терминалах АЦП используется для организации ввода информации для распознавания слуховых “образов”. Структурная схема речевого терминала содержит: ЦАП - для синтеза речи; фильтр нижних частот -ФНЧ; полосовой фильтр - ПФ; блок анализа и кодирования - БАК, где обработка сигнала выполняется методами дифференциальной импульсно-кодовой модуляции и выделения параметров линейного предсказания; блок синтеза и восстановления речевого сигнала - БСВ, осуществляющий операцию декодирования речевого сигнала в соответствии с заданной программой; блок распознавания образа (БРО), построенный на матричной БИС и выполняющий параллельную обработку вектора параметров речевого сигнала.

Очевидно, что в объеме данного учебного пособия рассмотреть все системы, использующие АЦП невозможно, поэтому основные направления и области применения АЦП кратко перечислены в табл. 5.2. В описании таблицы использованы следующие сокращения: ПС - АЦП последовательного счета; ПП - последовательного приближения; ПрП - прямого преобразования; И - двойного интегрирования; ПНЧ - с применением ГУН и , собственно, преобразователь напряжение - частота.

Сравнительные характеристики АЦП. Наибольшим быстродействием обладают АЦП прямого преобразования. Время преобразования tпр достигает 10 -20 нсек. Они используются для преобразования сигналов сверхбыстро протекающих процессов и сигналов телевизионного изображения (цифровое телевидение). Они отличаются высокой стоимостью и большой потребляемой мощностью. Функциональная схема АЦП прямого преобразования приведена на рис. 5.10. Она содержит 2n компараторов, делитель опорного напряжения и преобразователь позиционного кода в параллельный двоичный код. Промышленностью выпускаются 4, 6, 8 - разрядные АЦП прямого преобразования. Время преобразования этих АЦП определяется исключительно только временем распространения сигнала в компараторах tздкр и преобразователе кодов tздпр, т.е. tпр = tздкр + tздпр.

По своему быстродействию на втором месте находятся АЦП последовательного приближения (рис. 5.11). Время преобразования n- разрядного АЦП определяется как tпр = nТ + 3Т, где Т - период следования тактовых импульсов, соответствующий времени выборки одного кванта. Дополнительные 3 такта используются для старта( запуска) и формирования сигналов признака завершения процесса преобразования (сигнала “конец преобразования”).

Принцип работы АЦП последовательного приближения иллюстрируется на рис. 5.12. После запуска, на выходе АЦП устатанавливается число, соответствующее половине напряжения полной шкалы Uпш / 2. Это напряжение сравнивается с входным напряжением Uвх и, в зависимости от результата сравнения, компаратор вырабатывает два сигнала: U1 , когда Uвых ЦАП > Uвх и U2 при Uвых ЦАП < Uвх . Если Uвых ЦАП меньше, чем Uвх ЛСУ вырабатывает

команду, при которой к содержимому регистра последовательного приближения РПП прибавляется число, соответствующее половине напряжения, установленного в предыдущем такте. Если же Uвых ЦАП > Uвх , то из содержимого РПП это число вычитается (см. рис. 5.12). Это происходит до тех пор, пока напряжение приращения не станет равным DUкв , т.е. Un = DUкв =Uпш/2n..

Наибольшим времением преобразования (среди АЦП с использованием ЦАП) обладает АЦП последовательного счета tпр = 2n Т. Они проще в изготовлении и имеют наименьшую стоимость. Погрешность преобразования таких АЦП определяется, в основном, погрешностью ЦАП и может быть доведена до значений прецизионных преобразователей. АЦП последовательного счета переводит аналоговый сигнал в цифровой последовательно, начиная с младшего значащего разряда до цифрового кода на выходе, соответствующего уровню входного аналогового напряжения АЦП. Структурная схема такого АЦП приведена на рис. 5.13, а.

С генератора тактовых импульсов через электронный ключ ЭК, который открывается в момент выборки входного аналогового сигнала схемой запуска (СЗ), последовательность импульсов поступает на n- разрядный двоичный счетчик (СЧ). Выход счетчика является выходом АЦП и одновременно управляет схемой ЦАП, вырабатывающей ступенчато нарастающее напряжение (см. рис. 5.13, б). В момент, когда выходное напряжение ЦАП станет равным входному, компаратор (СР) вырабатывает сигнал, опрокидывающий триггер (ТГ). При этом, сигнал с выхода триггера закроет электронный ключ и остановит счетчик. Содержание счетчика Nсч после его остановки будет соответствовать числу, определяемому входным аналоговым сигналом

Nсч = Uвх/ DUкв.

Наибольшее число в счетчике соответствует входному напряжению, равному Uпш. При этом Nсч = 2n.

АЦП двойного интегрирования (интегрирующий АЦП). Способ двойного интегрирования позволяет хорошо подавлять сетевые помехи. На рис. 5.14 приведена функциональная схема АЦП двойного интегрирования. Работа его заключается в следующем. Счетчик запускается от генератора тактовых импульсов в момент поступления на интегратор входного сигнала Uвх , из которого за время интегрирования делается выборка. За время выборки напряжение на выходе интегратора Uвых и увеличивается. В момент tи прямое интегрирование заканчивается, входной сигнал от интегратора отключается и к его суммирующей точке подключается эталонный резистор. От времени tи до моментов t1 . . . t3 продолжается разряд конденсатора интегратора с посто-

янной скоростью. Интервалы времени от tи до нулевых отметок (t1 . . . t3) пропорциональны уровню входного сигнала. Существенным преимуществом преобразователя является простота компенсации наводок сети промышленного питания.

АЦП двойного интегрирования относится к наиболее медленно работающим преобразователям. Однако, высокая точность, низкий уровень шумов и низкая стоимость делают их незаменимыми для применения в щитовых приборах, мультиметрах, цифровых термометрах и т.п. Этому способствует также то, что результаты преобразования в интегрирующих АЦП часто представляются в десятичном коде или же в удобном виде для представления цифр десятичной системы счисления.

АЦП с применением ГУН, получивших название преобразователей напряжение - частота, обладают средним временем преобразования и используются, преимущественно, в измерительных системах, например, в системах измерения скорости и торможения автомобилей, измерения ухода частоты несущей в системах связи, высокоточных накопителях информации, помехоустойчивых системах передачи данных, фильтрах и др.

В табл. 5.3 приведены основные параметры наиболее популярных АЦП.

Цифро-аналоговые преобразователи

5.1. Цифро-аналоговые преобразователи (ЦАП)

ЦАП служит для преобразования цифровой информации в аналоговую форму, т.е. выходной сигнал ЦАП в общепринятых единицах измерения тока или напряжения (мВ, В, мА) соответствует численному значению входной кодовой комбинации.

Например, при подаче на вход ЦАП кодовой комбинации (в десятичном эквиваленте) равной 150 на его выходе при этом имеется напряжение 1500 мВ, это значит, что изменение значения входной кодовой комбинации (входного числа) на единицу приводит к изменению выходного напряжения на 10 мВ. В этом случае мы имеем ЦАП с шагом преобразования цифровой информации 10 мВ. Величина напряжения, соответствующая одной единице цифровой информации, называется шагом квантования Duкв. При подаче на вход ЦАП последовательной цифровой комбинации, меняющейся от 0 до N, на его выходе появится ступенчато-нарастающее напряжение (рис. 5.1). Высота каждой ступени соответствует одному шагу квантования Duкв.

Если число входной кодовой комбинации соответствует N, то выходное напряжение Uвых ЦАП = N´Duкв. Таким образом можно вычислить значение выходного напряжения для любой входной кодовой комбинации. Нетрудно убедиться в том, что Duкв является масштабным коэффициентом преобразователя, имеющим размерность тока или напряжения (так как цифровая комбинация на входе ЦАП размерности не имеет). Обычно, значение Duкв выбирают кратным десяти, что облегчает процесс пересчета соответствия преобразованного и исходного сигналов. Так как Duкв определяет минимальное значение выходного напряжения аналогового сигнала Uвых мин. = Duкв, при выборе его значения необходимо учитывать также шумовые факторы, погрешности усиления масштабирующих усилителей и компаратора.

Основные параметры ЦАП. Точность преобразования и качество работы ЦАП характеризуют следующие параметры: относительная разрешающая способность, абсолютная разрешающая способность, абсолютная погрешность преобразования, нелинейность преобразования, дифференциальная нелинейность, скорость преобразования (время одного преобразования) и максимальная частота преобразования.

1. Относительная разрешающая способность

dо =

,

здесь n- количество разрядов двоичного числа, подаваемого на вход АЦП (n - соответствует числу разрядных входов ЦАП). Относительная разрешающая способность - это обратная величина от максимального числа уровней квантования.

2. Абсолютная разрешающая способность

dа =

Duкв,

где Uпш - напряжение полной шкалы, соответствующее опорному напряжению ЦАП. Это напряжение можно считать равным максимальному выходному напряжению; 2n - 1 = N - количество ступеней квантования.

Численно абсолютная разрешающая способность равна шагу квантования Duкв.

3. Абсолютная погрешность преобразования dпш

показывает максимальное отклонение выходного напряжения Uвых в точке пересечения с идеальной характеристикой (прямой) на уровне напряжения полной шкалы (рис.5.2). Абсолютная погрешность преобразования оценивается в процентах или же в единицах младшего значащего разряда (МР). При оценке значения абсолютной погрешности преобразования знак напряжения не учитывается.

4. Нелинейность преобразования ЦАП dлн определяет максимальное отклонение реальной характеристики от идеальной (рис. 5.2) и оценивается также в процентах или в единицах младшего значащего разряда.

5. Дифференциальная нелинейность преобразования ЦАП dдф.лн численно равна максимальной разности двух соседних приращений (шагов квантования)

dдф.лн = Duкв 1 - Duкв2.

Дифференциальная нелинейность оценивается в младших значащих разрядах и обычно не превышает нескольких единиц мр.

Младший значащий разряд численно определяет минимальное значение выходного напряжения, т.е. квант напряжения. Для оценки дифференциальной нелинейности dдф.лн в процентах можно воспользоваться выражением

.

Время установления выходного напряжения или тока tуст - интервал времени от подачи входного двоичного входного кода до вхождения выходного сигнала в заданные пределы. Максимальная частота преобразования fпр - наибольшая частота дискретизации, при которой параметры ЦАП соответствуют заданным значениям.

Максимальная частота и время установления определяют быстродействие ЦАП.

Виды ЦАП условно можно разделить на две группы: с резисторными матрицами, безматричные ЦАП. В интегральном исполнении применяются только ЦАП с прецизионными резисторными матрицами, формирующими выходные сигналы путем суммирования токов.

ЦАП содержит элементы цифровой и аналоговой схемотехники. В качестве аналоговых элементов используются операционные усилители, аналоговые ключи (коммутаторы), резисторные матрицы и т.д.

Аналоговые элементы, входящие в состав ЦАП, практически полностью определяют его качественные и эксплуатационные параметры, основную роль при этом играют точность подбора номиналов резисторов резисторной матрицы и параметров операционного усилителя (ОУ).

Операционный усилитель представляет собой усилитель постоянного тока, имеющий коэффициент усиления по напряжению более тысячи. Он имеет дифференциальный входной каскад, т.е. имеет два входа: инвертирующий и неинвертирующий.

Своему названию ОУ “обязан” аналоговым вычислительным машинам, так как первоначально он был ориентирован на моделирование различных математических операций. Появление ОУ в виде интегральных микросхем привело к быстрому росту популярности ОУ в реализации аналоговой и гибридной электронной схемотехники. Условное обозначение ОУ показано на рис. 5.3.

Благодаря большому коэффициенту усиления (современные ОУ имеют коэффициент усиления К=105 ...106) и малым входным токам, усилители, построенные на базе ОУ, обладают уникальными свойствами. В частности, параметры многих устройств определяются только внешними цепями - цепями обратной связи, соединяющими выход ОУ с его входом. Например, коэффициент усиления усилителя, схема которого показана на рис. 5.4 (а), определяется с высокой точностью отношением сопротивлений двух резисторов К=-Rос/R.

Если на инвертирующий вход усилителя на ОУ подать сигнал от нескольких источников (рис. 5.4, б), то выходной сигнал определяется как произведение суммы входных токов на величину сопротивления резистора обратной связи

Uвых = -Rос(Iвх1+Iвх2+. . . . +Iвх.n).

Входной ток от каждого источника определяется как отношение

Iвх=Uвх/Ri,

где Ri - сопротивление резистора в цепи i-того входа.

Свойство ОУ суммировать входные токи с последующим преобразованием в напряжение широко используется при построении ЦАП и АЦП. На базе ОУ можно построить компараторы напряжения (сравнивающие устройства). При использовании ОУ в качестве компаратора напряжения на один его вход подается опорное напряжение Uоп, на второй - напряжение обрабатываемого (преобразуемого) сигнала Ux. При соответствующих условиях на выходе компаратора формируется сигнал логической“1”, если (Uоп - Ux) >Duкв, и логического “0”, если (Uоп - Ux)<Duкв (рис. 5.5). Шаг квантования Duкв обычно выбирается в пределах 5 . . . 10 мВ. Значение опорного напряжения и время установки компартора зависят от конкретного типа используемой интегральной микросхемы и условий его эксплуатации.

При построении ЦАП и АЦП применяются аналоговые ключи, коммутирующие цепи аналоговых сигналов под воздействием управляющих цифровых сигналов. Токи, коммутируемые электронными аналоговыми ключами, не превышают 10 . . . 50 мА. Относительно высокое сопротивление открытого ключа (50 - 600 Ом) требует наличия высокоомной нагрузки, что обеспечивается высокоомным входным сопротивлением ОУ.

При реализации ЦАП в интегральном исполнении большие трудности вызывает подгонка высокоточных резисторов с сопротивлениями, отличающимися по номиналам друг от друга на несколько порядков. Поэтому, в интегральном исполнении применяются исключительно резистивная матрица R-2R. В качестве примера рассмотрим четырехразрядный ЦАП, использующий схему суммирования токов на ОУ (рис. 5.6).

Относительная разрешающая способность рассматриваемого ЦАП:

dо =

= 0,0625.







Абсолютная разрешающая способность определяется при известном значении опорного напряжения Uоп.

Наиболее удобными значениями Uоп являются напряжения, кратные степени двойки, т.е. 10,24 В, 5,12 В, 2,56 В и т.д.

Если принять значение опорного напряжения равным 10,24 В, то абсолютная разрешающая способность (DUкв) определяется как:

DUкв=0,0625 × 10,24 = 0,625В.

Сопротивление резистора в цепи ключа, управляемого старшим разрядом двоичного кода, должно быть в два раза больше сопротивления резистора обратной связи Rос. Сопротивление каждого последующего младшего разряда в два раза больше, чем сопротивление соседнего старшего разряда. Отсюда следует, что с увеличением количества разрядов цифровых входов ЦАП резко увеличивается соотношение сопротивлений резисторов нулевого и самого старшего разрядов (R0=2nRn):

R0/Rn=2n = T.

Если n=8, то это отношение составляет 256. Увеличение Т может привести к чрезмерному увеличению сопротивления резистора младшего разряда или же к сильному уменьшению номинала резистора самого старшего разряда. Поэтому ЦАП с резистивной матрицей R-2nR применяется при небольшом количестве разрядов (при n<8). При больших Т затруднительным становится также изготовление резистивных матриц в интегральном исполнении. Известно, что номиналы резисторов в интегральном исполнении не должны превышать 50...100 кОм. Поэтому, в ЦАП, выполненных по интегральной технологии, в основном применяются резистивные матрицы R-2R. Функциональная схема ЦАП с матрицей R-2R показана на рис. 5.7.

Напряжение на выходе ЦАП (рис. 5.7) определяется как:

.

Чтобы выполнить условие формирования выходного напряжения в соответствии с двоичным кодом входного числа, необходимо получить равенство Rос=R, тогда

UвыхЦАП= Uоп

.

Дробные члены суммы играют роль весовых коэффициентов, а шаг квантования определяется отношением DUкв=Uоп/2n. На рис. 5.7 символы “0” и “1” перед электронными ключами показывают на состояние ключа при подаче на цифровые входы ЦАП логического “0” или “1”, соответственно.

Промышленностью ЦАП выпускаются в виде интегральных микросхемы и содержат в своем составе резистивную матрицу R-2R, электронные ключи и резистор обратной связи Rос. Для подключения токосуммирующего операционного усилителя имеются специальные выводы. Схема десятиразрядного ЦАП, построенного на базе ИМС К572ПА1, показана на рис. 5.8. ЦАП типа К572ПА1 может управляться кодом, полученным с выходов дискретных интегральных схем типов КМОП и ТТЛ. В последнем случае выходные уровни, соответствующие сигналам уровня логической “1”, должны быть повышены путем соединения выходов ТТЛ инверторов с источником питания 5 В через резисторы сопротивлением 2 - 10 кОм. Непосредственное согласование входных управляющих уровней ЦАП с параметрами сигналов ТТЛ- схем можно достичь путем уменьшения напряжения питания ЦАП до 5 В. Однако при

этом возрастает погрешность ЦАП. Основные параметры наиболее широко используемых ЦАП приведены в табл. 5.1. В табл. 5.1 использованы следующие обозначения: n- число разрядов управляющего кода; tуст - время установления выходного напряжения; Iвых - максимальный выходной ток; dлн - нелинейность преобразования ЦАП; Uп - напряжение питания; Uоп - опорное напряжение.

Функциональные цифроаналоговые преобразователи

5.3. Функциональные цифроаналоговые преобразователи

Цифроаналоговые преобразователи (ЦАП) широко применяются для преобразования сигналов в информационно-измерительной технике, радиотехнике и приборостроении. Они являются мощным средством увеличения точности отсчета. Однако существующие ЦАП могут выполнять только линейное преобразование вида Uвых=N´Uоп. В то же время в различных областях техники необходимо с высокой точностью воспроизводить нелинейные функциональные зависимости. Например, такая необходимость возникает при построении цифроуправляемых фазовращателей и калибраторов фазы, так как зависимость фазового сдвига от изменения регулируемой величины всегда нелинейна. Наиболее предпочтительный способ для осуществления этой операции – использование ЦАП. Аналогичная задача встречается в радиотехнике при компандировании сигнала.

Для воспроизведения нелинейных функциональных зависимостей и моделирования их с помощью линейных ЦАП можно использовать кусочно-линейную аппроксимацию и аппроксимацию степенными рядами. Каждый из упомянутых видов аппроксимации предполагает свой способ аппаратной реализации. Однако оба способа для увеличения дискретности воспроизводимой функции используют стандартные многоразрядные ЦАП.

Рассмотрим первый способ, в котором применяется линейная аппроксимация воспроизводимой функциональной зависимости y= f(x) в интервале [a+i(b-a)/n, a+(i+1)(b-a)/n]. Здесь [a, b] - отрезок, который разбивается на интервалы, (b-a)/n – величина интервала аппроксимации функциональной зависимости f(x), i=0, 1, 2, ..., n-1 (i - номер интервала аппроксимации, n - число отрезков аппроксимации зависимости f(x)). Полагаем, что на отрезке аппроксимации функция неотрицательна, хотя данный способ может быть расширен и на отрицательные значения функции.

В качестве многоразрядного линейного ЦАП необходимо выбрать любой умножающий ЦАП с постоянным входным сопротивлением R0. Например, ЦАП, построенный на резисторной матрице R-2R и управляемый двоичным кодом, или делитель напряжения с шунтирующими декадами, управляемый десятичным кодом.

На рис. 5.15 приведена схема, иллюстрирующая применение линейной аппроксимации для воспроизведения функциональной зависимости f(x).

Функциональный ЦАП с линейным преобразованием управляющего кода

5.4. Функциональный ЦАП с линейным преобразованием управляющего кода

Второй способ, использующий степенную аппроксимацию, заключается в следующем. На рассматриваемом отрезке [a, b] функция f(x) заменяется многочленом

Pn(x)=

Моделирование многочлена осуществляется каскадно соединенными ЦАП (рис. 5.18).

Рис. 5.18. Схема функционального цифро-аналогового преобразователя

В качестве ЦАП, изображенных на схеме, применяют умножающие ЦАП, которые могут работать с двухполярным опорным напряжением. Выходное напряжение таких ЦАП определяется по формуле:

где N - текущий цифровой код, который изменяется в пределах от 0 до Nmax-1; Nmax=2m, m - разрядность ЦАП; R - сопротивление матрицы резисторов; RN - сопротивление резистора в цепи обратной связи ОУ ЦАП; Uоп - опорное

напряжение. Отношение

называют масштабным коэффициентом или масштабным множителем. Его можно

изменять в широких пределах, изменяя RN.

В схеме, приведенной на рис. 5.18, при подаче на цифровые входы ЦАП кода N, на выходе 1-го ЦАП формируется напряжение, равное:

U1=- UопA

Это напряжение является входным для 2-го ЦАП, а напряжение на его выходе будет определяться соотношением:

U2=- U1A

=Uоп(- А

)2.

Продолжая этот ряд, для k-го ЦАП можно записать:

Uk = Uоп(- А

)k.

Напряжения с выходов ЦАП через резисторы R1, R2, ..., R5 подаются на вход сумматора А2. Для обеспечения необходимого знака, напряжения с выходов первого и пятого ЦАП проходят через инвертор А1. Дополнительно на сумматор через резистор R0 подается опорное напряжение. На выходе сумматора формируется напряжение Uвых:

Uвых=- (

);

или, с учетом предыдущего уравнения:

Uвых=- Uоп

Если обозначить

, то последнее уравнение примет вид:

Uвых=- Uоп(a0+a1x+a2x2+а3х3+а4х4+a5 x5)» - Uоп f(x).

Коэффициенты многочлена, реализуемого данной схемой, имеют следующие знаки: а0>0, а1>0, а2>0, а3<0, а4>0, а5>0. Если коэффициенты имеют другие знаки, то схема претерпевает лишь незначительные изменения. Таким образом, мы получаем выходное напряжение пропорциональное аппроксимируемой функции f(x).

Необходимо указать на ограничение, которое накладывается каскадным включением ЦАП на диапазон изменения масштабного коэффициента А. При подаче на цепочку ЦАП кода, близкого к Nmax, выходное напряжение k-го ЦАП пропорционально Uоп(- A)k. Для А>1 эта величина возрастает по геометрической прогрессии и может приводить к насыщению операционных усилителей. Поэтому выгодно устанавливать А равным 1 и аппроксимировать функцию исходя из того, что аргумент х изменяется от 0 до 1.

Из вышесказанного следует, что для воспроизведения многочлена Pn(x) степени n необходимо n каскадно включенных ЦАП. Коэффициенты многочлена реализуются подбором резисторов R, R0 ,R1, ... Rk, а знаки слагаемых устанавливаются при помощи инвертора.

Для того чтобы погрешность, вызванная аппроксимацией (методическая погрешность), была минимальна, необходимо соответствующим образом подобрать коэффициенты многочлена.

Рассмотрены три метода вычисления этих коэффициентов.

Наиболее распространенный метод аппроксимации функции f(x) – ее разложение в ряд Тейлора. В общем виде это разложение функции f(x) в окрестности точки х0 осуществляется по формуле:

.

Разложение функции в ряд Тейлора не является единственным. Существует возможность разложить функцию в ряд по обобщенным многочленам, например, по многочленам Лежандра, Чебышева, Якоби, Эрмита или Лагерра. Здесь мы остановимся на многочленах Чебышева, поскольку они дают наилучшее приближение.

Для нахождения коэффициентов Ck разложения по многочленам Чебышева

используем следующие формулы:

, k > 0.

Подставляя вместо степеней х их выражения через многочлены Чебышева, а затем, приводя подобные члены при многочленах одной степени, получим искомый многочлен Pn(x)=

.

Оценить погрешность, даваемую разложением функции f(x) в ряд по многочленам Чебышева в общем виде, очень трудно. Но согласно общим теоремам теории аппроксимации это разложение дает наилучшее приближение из всех возможных. Необходимо также отметить, что разложение функции f(x) по многочленам Чебышева возможно только для функций, имеющих непрерывную первую производную на отрезке [-1, 1]. Это условие обеспечивает сходимость ряда к функции f(x). Для всех простейших функций это условие выполняется.

Следующий метод основан на теории интерполяции. В этом случае строят многочлен, который в n+1 заданных точках х0, х1, . . . xn, принимает значения f(x0), f(x1), . . . f(xn), а в остальных точках отрезка [a, b], принадлежащего области определения f(x), приближенно представляет функцию f(x) с той или иной степенью точности. Для нахождения коэффициентов многочлена ak составляется система уравнений:

, ( i = 0, 1, 2, . . . , n ),

которая легко решается, например, методом Крамера.

Пример.

Калибратор фазы с линейным преобразованием

управляющего кода в фазовый сдвиг

Широкое распространение получают калибраторы фазы, принцип действия которых заключается в суммировании двух синусоидальных напряжений, сдвинутых одно относительно другого на 90°. Диапазон регулирования фазового сдвига при этом составляет 0-90°, а его расширение до 360° осуществляется введением коммутатора опорных напряжений.

При регулировании фазового сдвига в пределах 0-90° выходное напряжение калибратора фазы формируется в соответствии с зависимостью

, (*)

где Uвх - амплитуда опорных напряжений;

k1 и k2 - весовые коэффициенты.

Амплитуда и фаза выходного напряжения связаны с весовыми коэффициентами k1 и k2 соотношениями

;

Калибраторы фазы, управляемые цифровым кодом, должны обеспечивать линейное преобразование управляющего кода в фазовый сдвиг выходного напряжения. Кроме того, в большинстве практических случаев необходимо обеспечить постоянство амплитуды выходного напряжения во всем диапазоне регулирования фазового сдвига. Для выполнения этих требований весовые коэффициенты k1 и k2 должны быть связаны с управляющим кодом нелинейными зависимостями.

В калибраторе фазы, структурная схема которого представлена на рис.5.19, выходное напряжение является суммой двух синусоидальных напряжений

, сдвинутых одно относительно другого на 90°. Они формируются из входного синусоидального напряжения

цепью каскадно включенных цифроаналоговых преобразователей ЦАП1 - ЦАП7 и инвертирующими сумматорами А1 - А4.

Передаточная функция i-го ЦАП

выражается линейной зависимостью

,

где bi - масштаб преобразования i-го ЦАП;

N и Nmax - текущее и максимальное значения управляющего кода.

Рис. 5.19. Калибратор фазы с линейным преобразованием управляющего

кода в фазовый сдвиг

Применяемые в калибраторе фазы ЦАП имеют малое выходное сопротивление, что допускает их каскадное включение без нарушения нормального режима работы каждого отдельно взятого ЦАП.

Поэтому передаточную функцию n каскадно включенных ЦАП с достаточной степенью точности можно записать в виде

На вход первого ЦАП, являющегося входом калибратора фазы, с внешнего генератора поступает синусоидальное напряжение

. Из него цепью каскадно включенных ЦАП формируются напряжения, амплитуды Un которых связаны с управляющим кодом соотношением

где

Напряжения

с выходов ЦАП и входное напряжение используются для формирования двух синфазных напряжений

, причем напряжение

формируется из входного напряжения и напряжений с выходов ЦАП с четными номерами, а выходные напряжения нечетных ЦАП используются для формирования напряжения

. Полагая весовые коэффициенты суммируемых напряжений

равными единице и учитывая дополнительное инвертирование соответствующих напряжений сумматорами А1 и А3, зависимости амплитуды напряжений

от управляющего кода в соответствии с (4.5) можно представить в виде

Us = - Uвх(a1x- a3x3+a5x5- a7x7) = Uвхk2;

Uc = - Uвх(1- a2x2+a4x4- a6x6) = Uвхk1.

Таким образом, амплитуды напряжений

связаны с амплитудой синусоидального напряжения

, поступающего на вход калибратора фазы, коэффициентами k1 и k2, которые в свою очередь имеют нелинейную зависимость от управляющего кода.

k1 = 1- a2x2+a4x4- a6x6;

k2 = a1x- a3x3+a5x5- a7x7.

Чтобы получить фазовый сдвиг 90° между напряжениями

, одно из них,

, подается на вход фазовращателя ФВ, в результате чего на входы сумматора А5 поступают напряжения Uc и jUs. Выходное напряжение сумматора А5, являющееся выходным напряжением калибратора фазы, описывается соотношением (*).

Фаза

определяется управляющим кодом, а амплитуда выходного напряжения зависит только от амплитуды входного напряжения Uвх (в рассмотренном случае Uвых=Uвх).

Разность между расчетными и заданными значениями фазы и амплитуды выходного напряжения будет тем меньше, чем точнее моделируются функциональные зависимости cosx и sinx.

Функции cosx и sinx могут быть представлены в виде суммы степенного ряда, причем тем точнее, чем больше членов степенного ряда при этом используется и чем меньше диапазон изменения аргумента x. Когда заданы число членов ряда и диапазон изменения переменной x, задача минимизации погрешности моделирования сводится к точному вычислению коэффициентов при суммирующихся членах ряда.

В табл. 5.5 приведены значения коэффициентов an, рассчитанные для трех случаев, когда высшая степень x и число ЦАП в схеме калибратора фазы соответственно равны семи, шести и пяти.

Методическая фазовая погрешность и нестабильность амплитуды выходного напряжения определяются соотношениями

.

Графики этих зависимостей приведены на рис. 5.20 (а, б) (где m - число ЦАП в схеме), а их максимальные значения указаны в табл. 5.5.

Таблица 5.5.

Коэффициенты an	d Uвых, %	D j, °
a1 = 1,000 a2 = 0,4999 a3 = 0,1666 a4 = 0,0416 a5 = 0,0083 a6 = 0,0013 a7 = 0,0002	0,005	0,003
a1 = 1,000 a2 = 0,4999 a3 = 0,1661 a4 = 0,0416 a5 = 0,0076 a6 = 0,0013	0,016	0,005
a1 = 1,000 a2 = 0,4967 a3 = 0,16605 a4 = 0,03705 a5 = 0,00761	0,06	0,06

Рис. 5.20. Зависимости погрешности фазового сдвига Dj (а) и модуля dUвых напряжения выхода (б)

Анализ полученных результатов показывает, что уже при использовании шести ЦАП можно построить калибратор фазы с высокими метрологическими характеристиками. Погрешность калибратора фазы в основном будет определяться погрешностью настройки ЦАП на заданный масштаб преобразования, паразитными фазовыми сдвигами в ЦАП и сумматорах на высоких частотах, точностью поддержания фазового сдвига 90°.

Экспериментальная проверка макета калибратора фазы показала, что в диапазоне 30 Гц - 20 кГц основная погрешность не превышает 0,1° и достигает максимального значения на верхней частоте указанного диапазона (испытания макета проводили с использованием калибратора фазы, прошедшего метрологическую аттестацию во ВНИИМ).

Функциональный цифроаналоговый преобразователь

Значения сопротивлений R1i, R2i, R0 связаны между собой соотношениями:

Напряжения в схеме рис. 5.15 будут распределяться следующим образом:

где U - напряжение, подводимое к нелинейному ЦАП.

С помощью линейного ЦАП выходное напряжение Uвых изменяется от величины

до

, приближенно воспроизводя в i-ом интервале зависимость f(x) c заданным шагом квантования. Для изменения интервала регулирования функциональной зависимости f(x) (старший разряд нелинейного ЦАП) используется ключ П (рис. 5.15).

Естественно, что при таком построении функционального ЦАП последний имеет методическую погрешность, вызванную линейной аппроксимацией функциональной зависимости f(x) в интервале [

]. Эта погрешность определяется выражением

где y1i - уравнение прямой, аппроксимирующей зависимость f(x) в интервале [

]. Введем обозначение

, тогда уравнение прямой запишется в виде:

Здесь

£ x £

. Методическая погрешность воспроизведения функции f(x) будет зависеть в первую очередь от ее вида и выбранного отрезка аппроксимации, а также от номера и количества участков аппроксимации.

Нелинейные ЦАП, аппроксимирующие функции sinj и cosj, широко применяются при построении калибраторов фазы и фазовращателей (синусно-косинусные потенциометрические фазовращатели), в которых для формирования напряжения выхода реализуется соотношение:

Пример.

В качестве примера рассмотрим построение функционального цифроаналогового преобразователя – дискретного аналога синусно-косинусного потенциометра.

Известные синусно-косинусные потенциометры нашли применение в радиотехнике, информационно-измерительной технике. Они используют профилированную намотку провода и имеют скользящий контакт, что нетехнологично, не позволяет получить хорошие метрологические характеристики и не дает возможность применить их в микроэлектронике.

Выполнение синусно- косинусного потенциометра из набора резисторов и ключей привело бы к необходимости применения большого количества резисторов разных номиналов и ключей. Так, для дискретного потенциометра, воспроизводящего синусную зависимость сопротивления от изменения входного кода в диапазоне от 0 до 90° и дискретностью 0.1°, потребовалось бы 900 резисторов и 901 ключ.

Вполне очевидно, что подобные дискретные синусные потенциометры очень громоздки и, кроме того, при такой реализации синусного потенциометра невозможно производить поразрядное регулирование воспроизводимой функциональной зависимости.

От этих недостатков свободна схема, приведенная на рис. 5.16, построенная на базе нелинейного ЦАП — цифро-аналогового преобразователя, воспроизводящего нелинейную зависимость sinj.

Рис. 5.16. Функциональный ЦАП - дискретный аналог синусного потенциометра

С помощью сдвоенного ключа линейный многоразрядный ЦАП, подключается к резисторам R1i и R2i - и образует преобразователь, моделирующий зависимость sinj в интервале от ip/2n до (i+1)p/2n. Здесь p/2n - интервал аппроксимации функциональной зависимости sinj, i=0,1,2,...,n-1 (i-номер интервала аппроксимации, n-число отрезков аппроксимации зависимости sinj в интервале от 0 до p/2 ). В качестве многоразрядного линейного ЦАП можно использовать любой ЦАП с постоянным входным сопротивлением R0.

Значения сопротивлений R1i, R2i, R0 определяются из соотношений:

Напряжения в схеме рис. 5.16 будут распределяться следующим образом:

где U- напряжение, подводимое к дискретному аналогу синусного потенциометра – функциональному ЦАП.

С помощью линейного ЦАП выходное напряжение Uвых изменяется от величины

до

, приближенно воспроизводя в i-ом интервале зависимость sinj необходимым числом разрядов. Для изменения интервала регулирования функциональной зависимости sinj (старший разряд нелинейного ЦАП) используется ключ П (рис. 5.16).

Естественно, что при таком построении дискретного аналога синусного потенциометра последний имеет методическую погрешность, вызванную линейной аппроксимацией зависимости sinj в интервале [ip/2n, (i+1)p/2n]. Эта погрешность определяется выражением

,

где y1i - уравнение прямой , аппроксимирующей зависимость sinj в интервале [ip/2n, (i+1)p/2n]:

.



Здесь ip/2n £ j £ (i+1)p/2n.

На рис. 5.17 приведена зависимость методической погрешности воспроизведения зависимости sinj внутри интервала аппроксимации (D) для n=9. В этом случае старший разряд регулирования фазового сдвига составляет 10° . Для удобства введена новая переменная k из соотношения

j = (i+k)×p/2n.   Здесь 0 £ k £ 1.

Рис. 5.17 Распределение методической погрешности дискретного аналога синусного потенциометра внутри интервалов аппроксимации (n=9).

Наибольший интерес представляет максимальная погрешность, получаемая при аппроксимации последнего интервала зависимости sinj. В табл. 5.4 приведены максимальные величины погрешности в зависимости от числа интервалов аппроксимации.

Таблица 5.4.

n	3	9	18	36	72
D, %	3,29	0,38	0,09	0,02	0,006

Так, в случае n=9, она составляет величину менее 0,4 %, что может быть приемлемо для многих практических применений.

В случае одновременного использования синусного и косинусного преобразователей, как это сделано в работе для построения фазовращателя, методическая погрешность воспроизведения фазового сдвига получается небольшой, поскольку погрешности преобразователей имеют один знак. Так, при подекадном регулировании фазового сдвига (n=9) методическая погрешность, вызванная аппроксимацией зависимостей sinj и cosj , составляет всего полминуты.

Дискретный аналог синусного потенциометра (рис. 5.16) дает возможность изменять зависимость sinj в пределах одного квадранта. Все эти же элементы используются и для регулирования зависимости sinj во всех четырех квадрантах, но в третьем и четвертом квадрантах для получения отрицательных величин используется инвертор или во входной цепи (инвертируется входное напряжение), или в выходной цепи (инвертируется выходное напряжение). Кроме того, все элементы схемы рис. 5.16 применяются и для построения дискретного аналога косинусного потенциометра, поскольку cosj=sin(p/2+j). Таким образом, схема, приведенная на рис. 5.16, может почти полностью обеспечить одновременное моделирование и синусного, и косинусного преобразователей.

Рассмотренный способ применим для построения цифроуправляемых потенциометрических и мостовых фазовращателей.

Поясните физический смысл основных параметров

Вопросы и задания
5.1. Поясните физический смысл основных параметров ЦАП и АЦП. От каких внешних и внутренних факторов они зависят?
5.2. Какие физические ограничения препятствуют бесконечному уменьшению шага квантования в ЦАП и АЦП?
5.3. Нарисуйте схему простейшего 5-ти разрядного ЦАП с резисторной матрицей R - Rn.
5.4. Каким быстродействием должен обладать АЦП для удовлетворительного преобразования в цифровую форму сигналов речи с верхней частотой до 5 кГц?
5.5. Дайте сравнительные характеристики всем типам АЦП. Укажите, какой тип АЦП может преобразовать телевизионные сигналы.
5.6. Нарисуйте схему простейшего АЦП последовательно счета с использованием ЦАП.
5.7. Нарисуйте схемы функциональных ЦАП и расскажите их принцип действия.

Классификация интегральных микросхем

6.1. Классификация интегральных микросхем

В зависимости от технологии изготовления интегральные микросхемы могут быть полупроводниковыми, пленочными или гибридными.

Полупроводниковая микросхема -микросхема, все элементы и межэлементные соединения которой выполнены в объеме и на поверхности полупроводника.

Пленочная микросхема - микросхема, все элементы и межэлементные соединения которой выполнены только в виде пленок проводящих и диэлектрических материалов. Вариантами пленочных являются тонкопленочные и толстопленочные микросхемы.

Различие между тонкопленочными и толстопленочными микросхемами может быть количественным и качественным. К тонкопленочным условно относят микросхемы с толщиной пленок менее 1 мкм, а к толстопленочным - микросхемы с толщиной пленок свыше 1 мкм.

Гибридная микросхема - микросхема, содержащая кроме элементов простые и сложные компоненты (например, кристаллы микросхемы полупроводниковых микросхем). Одним из видов гибридной микросхемы является многокристальная микросхема.

В зависимости от функционального назначения интегральные микросхемы делятся на аналоговые и цифровые. Аналоговые микросхемы предназначены для преобразования и обработки сигналов, изменяющихся по закону непрерывной функции. Частным случаем этих микросхем является микросхема с линейной характеристикой, линейная микросхема. С помощью цифровых микросхем преобразуются, обрабатываются сигналы, изменяющиеся по закону дискретной функции. Частным случаем цифровых микросхем являются логические микросхемы, выполняющие операции с двоичным кодом, которые описываются законами логической алгебры.

Минимальный состав комплекта интегральных микросхем, необходимый для решения определенного круга аппаратурных задач, называется базовым.

После появления микропроцессоров были введены дополнительные термины. Микропроцессор определен как программно-управляемое устройство, осуществляющее процесс обработки цифровой информации и управления им. Это устройство изготовлено на основе одной или нескольких больших интегральных схем (БИС).

Микропроцессорной названа микросхема, выполняющая функцию МП или его часть. Совокупность этих и других микросхем, совместимых по архитектуре, конструктивному исполнению и электрическим параметрам, называется микропроцессорным комплектом.

В последние годы в классификацию ИС вводятся новые понятия: микросхемы общего назначения, заказные и полузаказные.

Заказная микросхема - микросхема, разработанная на основе стандартных и (или) специально созданных элементов узлов по функциональной схеме заказчика предназначена для определенной радиоэлектронной аппаратуры (РЭА).

Полузаказная интегральная микросхема - микросхема, разработанная на основе базовых кристаллов ( в том числе матричных).

Система условных обозначений микросхем. Аналоговые и цифровые интегральные микросхемы разрабатываются и выпускаются предприятиями - изготовителями в виде серий. Каждая серия отличается степенью комплектности и содержит несколько микросхем, которые, в свою очередь, подразделяются на типономиналы. К серии микросхем относят совокупность типов микросхем, которые могут выполнять различные функции, но имеют единое конструктивно-технологическое исполнение и предназначены для совместного применения. Как правило, с течением времени состав перспективных серий расширяется.

Тип интегральной микросхемы - интегральная микросхема конкретного функционального назначения и определенного конструктивно-технологического и схемотехнического решения, имеющая свое условное обозначение. Под типономиналом интегральной микросхемы понимается микросхема конкретного типа, отличающаяся от других микросхем того же типа одним или несколькими параметрами.

Группа типов микросхем - совокупность типов микросхем в пределах одной серии, имеющих аналогичное функциональное назначение и принцип действия, свойства которых описываются одинаковым или же близким составом электрических параметров.

Основные электрические параметры микросхем

6.3. Основные электрические параметры микросхем

Цифровые микросхемы развивались в следующей последовательности: резистивно-транзисторная логика (РТЛ), диодно-транзисторная логика (ДТЛ), транзисторно-транзисторная логика (ТТЛ), эмиттерно-связанная логика (ЭСЛ), транзисторно-транзисторная логика с диодами Шотки (ТТЛШ), интегрально-инжекционная логика (И2Л). В этих определениях слово “логика” подразумевает понятие “электронный ключ”.

Все перечисленные выше логические микросхемы выполнены на базе биполярных транзисторов. Наряду с ними широкое распространение получили цифровые микросхемы на МОП - структурах (на транзисторах p- и n-типов с обогащенным каналом, КМОП - схемы на дополняющих транзисторах). Серии РТЛ, РЕТЛ промышленностью в настоящее время не выпускаются, но еще используются только для комплектации серийной РЭА. Наиболее широкое распространение в современной аппаратуре получили серии микросхем ТТЛШ, ЭСЛ и схемы на КМОП-структурах, так как они отличаются более высоким уровнем интеграции и обладают большим функциональным разнообразием.

Можно выделить три этапа развития микросхем, входящих в состав стандартных серий для создания цифровых устройств различного назначения.

I этап (1969 - 1975 гг.). В состав стандартных серий входили микросхемы малой степени интеграции, выполняющие простейшие логические функции, например серия К155.

II этап (1976 - 1980 гг.). Появились серии с улучшенными характеристиками, такие как 531, 555, 500, К561, К1561 и другие, что привело к ограниченному применению серий 131, 158, 137, 187.

III этап (1981 - 1987 гг.). Разработка микросхем большой степени интеграции, микропроцессорных комплектов, запоминающих устройств, полузаказных БИС на основе матричных кристаллов.

Параметры микросхем конкретной серии в основном определяются параметрами базовых элементов логики. К основным параметрам относятся: быстродействие; потребляемая мощность (Рпот); помехоустойчивость Uпом; коэффициент разветвления по выходу (нагрузочная способность) Краз; коэффициент объединения по входу Коб. Быстродействие определяется динамическими параметрами цифровых микросхем, к которым относятся: t1,0 - время перехода сигнала на выходе микросхемы из состояния логической “1” в состояние логического “0”; t0,1 -время перехода из состояния низкого уровня в состояние высокого уровня; t1,0здр - время задержки распространения при включении; t1,0зд -время задержки включения; t0,1здр - время задержки распространения при выключении; t0,1зд - время задержки выключения; tздрср - среднее время задержки распространения сигнала; fр - рабочая частота. Среднее время задержки распространения tэдрср = 0,5(t1,0здр + t0,1здр) является усредненным параметром быстродействия микросхемы, используемым при расчете временных характеристик последовательно включенных цифровых микросхем. На рис. 6.1 показаны уровни отсчета, определяющие параметры быстродействия цифровых микросхем.

В зависимости от технологии микросхем, мощности, потребляемые при состоянии логического нуля и при состоянии логической “1” могут отличаться. Поэтому, мощность, потребляемая логическими элементами в динамическом режиме, определяется как

Рпотср = 0,5(Р0пот + Р1пот),

где Р0пот - мощность, потребляемая микросхемой при состоянии выхода “0”, Р1пот - мощность при выходном состоянии “1”.

Некоторые логические элементы кроме статической средней мощности характеризуются мощностью, потребляемой на максимальной частоте переключения, когда токи в цепях питания возрастают во много раз. К таким схемам относятся микросхемы КМОП технологии, которые потребляют микроамперы, если нет переключающих сигналов.

Допустимый уровень напряжения помехи логического элемента определяется уровнем входного напряжения, при котором еще не происходит ложное срабатывание микросхемы.

В статическом режиме помехоустойчивость определяется по низкому U0пом и высокому U1пом уровням. Значения U0пом и U1пом определяют с помощью передаточных характеристик (рис. 6.2.). Как следует из рис. 6.2, напряжение помехи по высокому уровню определяется как разность минимального напряжения высокого уровня U1вхmin и напряжения в точке перегиба верхней кривой (точка В). Параметр U0пом определяется как разность напряжения низкого уровня U0вхmax.

Помехоустойчивость в динамическом режиме зависит от длительности, амплитуды и формы импульса помехи, а также от запаса статической помехоустойчивости и скорости переключения логического элемента.

Коэффициент разветвления по выходу Краз определяет число входов аналогичных элементов, которое может быть подключено к выходу предыдущего элемента без нарушения его работоспособности. С увеличением нагрузочной способности расширяются возможности применения цифровых микросхем и уменьшается число корпусов в разрабатываемом устройстве. Однако при этом ухудшаются помехоустойчивость и быстродействие микросхемы и возрастает потребляемая мощность.

Коэффициент объединения по входу Коб определяет максимальное число входов цифровых микросхем.

Пример условного обозначения полупроводниковой микросхемы:

Окончание табл.6.1

Пример условного обозначения полупроводниковой микросхемы: обозначение - ИЕ (счетчик) с порядковым номером серии 554 и номером разработки микросхемы в данной серии по функциональному признаку 7. Полное обозначение микросхемы 1554ИЕ7.

В последнее время при четырехзначном номере серии первую цифру порядкового номера серии устанавливают в зависимости от функционального назначения микросхем, входящих в серию. Например, цифра 0 определяет, что данная серия микросхем предназначена для работы в составе бытовой радиоэлектронной аппаратуры. Цифра 1 ставится на аналоговых микросхемах, цифра 4 - микросхемам ОУ, цифра 5 - цифровым микросхемам, цифра 6 - серии микросхем памяти, цифра 8 - сериям МП.
Если в конце условного обозначения стоит буква, то она определяет технологический разброс электрических параметров данного типономинала.
На микросхемах, используемых в устройствах широкого применения, в начале обозначения ставится буква К, например: К1533ИР22.
Для характеристики материала и типа корпуса перед цифровым обозначением серии могут быть добавлены следующие буквы: Р - пластмассовый корпус типа ДИП; М - металлокерамический корпус типа ДИП и т.д.

Все многообразие выпускаемых серий микросхем

6.2. Условные обозначения микросхем

Все многообразие выпускаемых серий микросхем согласно принятой системе условных обозначений по конструктивно-технологическому исполнению делится на три группы: полупроводниковые, гибридные, прочие. К последней группе относят пленочные микросхемы, которые в настоящее время выпускаются в ограниченном количестве, а также вакуумные и керамические. Указанным группам микросхем в системе условных обозначений присвоены следующие цифры: 1, 5, 7 - полупроводниковые (обозначение 7 присвоено бескорпусным микросхемам); 2, 4, 8 - гибридные; 3 - прочие микросхемы.

По характеру выполняемых функций микросхемы подразделяются на подгруппы (генераторы, модуляторы, триггеры, усилители, логические схемы и др.) и виды (преобразователи частоты, фазы, длительности, напряжения и др.). Классификация наиболее популярных микросхем по функциональному назначению приведена в таблице 6.1.

По принятой системе, обозначение микросхемы должно состоять из четырех элементов. Первый элемент - цифра, соответствующая конструктивно-технологической группе. Второй элемент - две-три цифры, присвоенные данной серии как порядковый номер разработки. Таким образом, первые два элемента составляют три-четыре цифры, определяющие полный номер серии микросхемы. Третий элемент - две буквы, соответствующие подгруппе и виду (табл. 6.1). Четвертый элемент - порядковый номер разработки микросхемы в данной серии, в которой может быть несколько одинаковых по функциональному признаку микросхем. Он может состоять как из одной цифры, так и из нескольких.

В качестве примера рассмотрим условное обозначение полупроводниковой микросхемы серии 1554ИР22. Из условного обозначения следует, что эта микросхема - регистр с порядковым номером 554 и номером разработки микросхемы в данной серии по функциональному признаку 22 выполнена по полупроводниковой технологии.